LARNet: Lie Algebra Residual Network for Profile Face Recognition

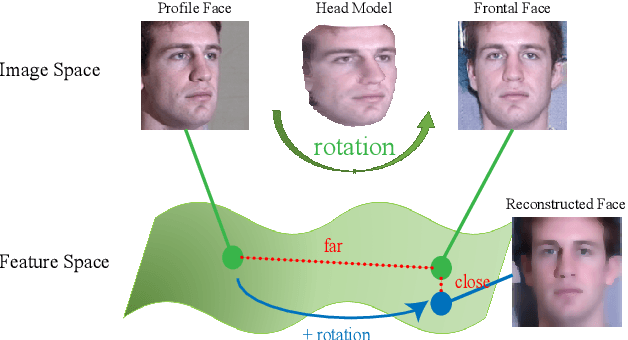
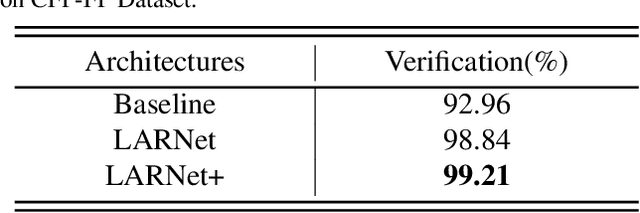
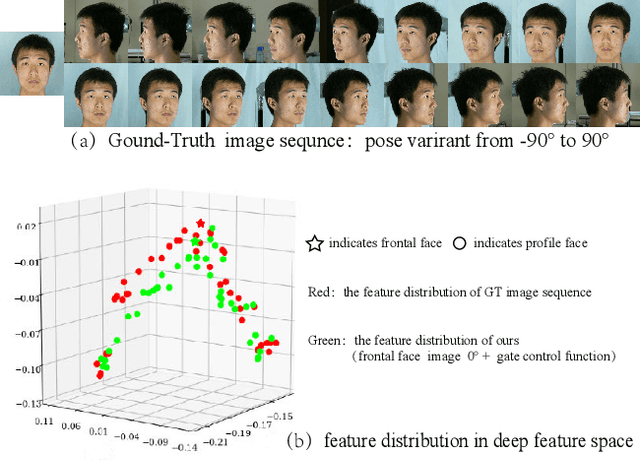
Due to large variations between profile and frontal faces, profile-based face recognition remains as a tremendous challenge in many practical vision scenarios. Traditional techniques address this challenge either by synthesizing frontal faces or by pose-invariants learning. In this paper, we propose a novel method with Lie algebra theory to explore how face rotation in the 3D space affects the deep feature generation process of convolutional neural networks (CNNs). We prove that face rotation in the image space is equivalent to an additive residual component in the feature space of CNNs, which is determined solely by the rotation. Based on this theoretical finding, we further design a Lie algebraic residual network (LARNet) for tackling profile-based face recognition. Our LARNet consists of a residual subnet for decoding rotation information from input face images, and a gating subnet to learn rotation magnitude for controlling the number of residual components contributing to the feature learning process. Comprehensive experimental evaluations on frontal-profile face datasets and general face recognition datasets demonstrate that our method consistently outperforms the state-of-the-arts.