Large Scale Training of Graph Neural Networks for Optimal Markov-Chain Partitioning Using the Kemeny Constant
Paper and Code
Dec 25, 2023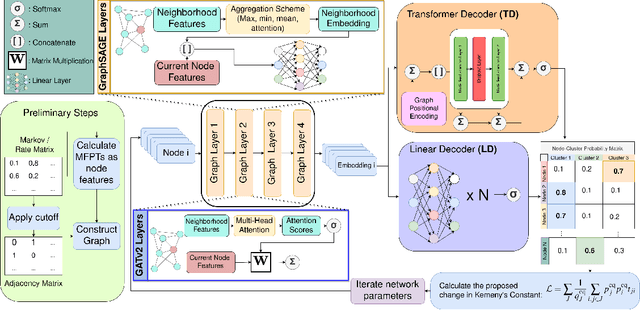
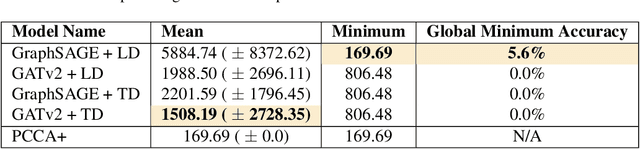
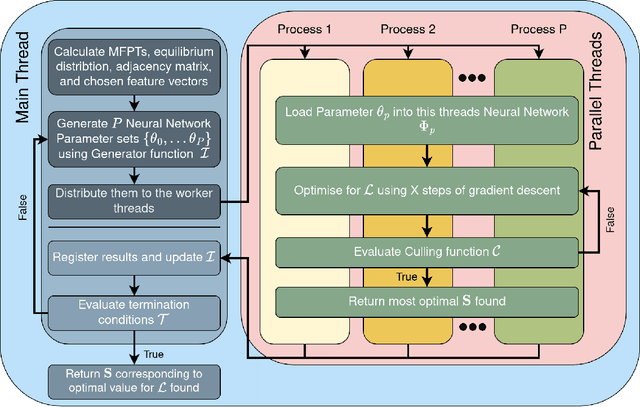
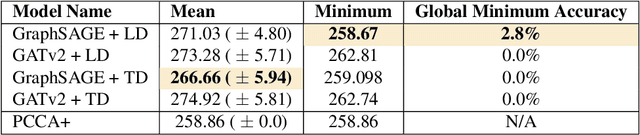
Traditional clustering algorithms often struggle to capture the complex relationships within graphs and generalise to arbitrary clustering criteria. The emergence of graph neural networks (GNNs) as a powerful framework for learning representations of graph data provides new approaches to solving the problem. Previous work has shown GNNs to be capable of proposing partitionings using a variety of criteria, however, these approaches have not yet been extended to work on Markov chains or kinetic networks. These arise frequently in the study of molecular systems and are of particular interest to the biochemical modelling community. In this work, we propose several GNN-based architectures to tackle the graph partitioning problem for Markov Chains described as kinetic networks. This approach aims to minimize how much a proposed partitioning changes the Kemeny constant. We propose using an encoder-decoder architecture and show how simple GraphSAGE-based GNNs with linear layers can outperform much larger and more expressive attention-based models in this context. As a proof of concept, we first demonstrate the method's ability to cluster randomly connected graphs. We also use a linear chain architecture corresponding to a 1D free energy profile as our kinetic network. Subsequently, we demonstrate the effectiveness of our method through experiments on a data set derived from molecular dynamics. We compare the performance of our method to other partitioning techniques such as PCCA+. We explore the importance of feature and hyperparameter selection and propose a general strategy for large-scale parallel training of GNNs for discovering optimal graph partitionings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge