Large Scale Spectral Clustering Using Approximate Commute Time Embedding
Paper and Code
Feb 29, 2012
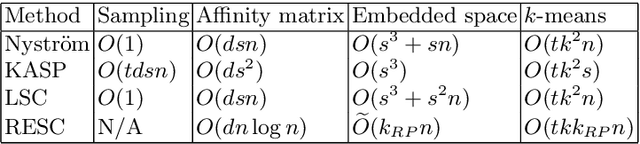

Spectral clustering is a novel clustering method which can detect complex shapes of data clusters. However, it requires the eigen decomposition of the graph Laplacian matrix, which is proportion to $O(n^3)$ and thus is not suitable for large scale systems. Recently, many methods have been proposed to accelerate the computational time of spectral clustering. These approximate methods usually involve sampling techniques by which a lot information of the original data may be lost. In this work, we propose a fast and accurate spectral clustering approach using an approximate commute time embedding, which is similar to the spectral embedding. The method does not require using any sampling technique and computing any eigenvector at all. Instead it uses random projection and a linear time solver to find the approximate embedding. The experiments in several synthetic and real datasets show that the proposed approach has better clustering quality and is faster than the state-of-the-art approximate spectral clustering methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge