Large-scale kernelized GRANGER causality to infer topology of directed graphs with applications to brain networks
Paper and Code
Nov 16, 2020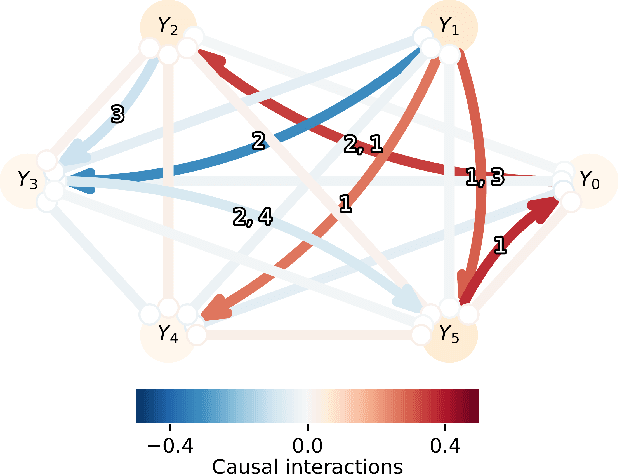
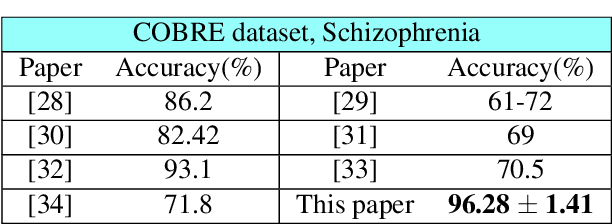
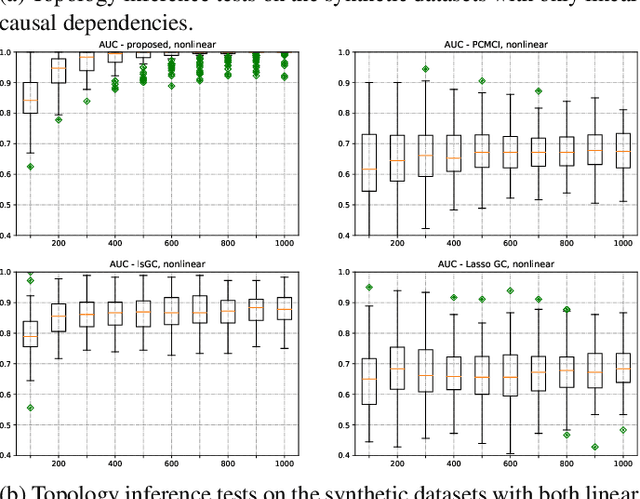
Graph topology inference of network processes with co-evolving and interacting time-series is crucial for network studies. Vector autoregressive models (VAR) are popular approaches for topology inference of directed graphs; however, in large networks with short time-series, topology estimation becomes ill-posed. The present paper proposes a novel nonlinearity-preserving topology inference method for directed networks with co-evolving nodal processes that solves the ill-posedness problem. The proposed method, large-scale kernelized Granger causality (lsKGC), uses kernel functions to transform data into a low-dimensional feature space and solves the autoregressive problem in the feature space, then finds the pre-images in the input space to infer the topology. Extensive simulations on synthetic datasets with nonlinear and linear dependencies and known ground-truth demonstrate significant improvement in the Area Under the receiver operating characteristic Curve ( AUC ) of the receiver operating characteristic for network recovery compared to existing methods. Furthermore, tests on real datasets from a functional magnetic resonance imaging (fMRI) study demonstrate 96.3 percent accuracy in diagnosis tasks of schizophrenia patients, which is the highest in the literature with only brain time-series information.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge