Label Smoothed Embedding Hypothesis for Out-of-Distribution Detection
Paper and Code
Feb 09, 2021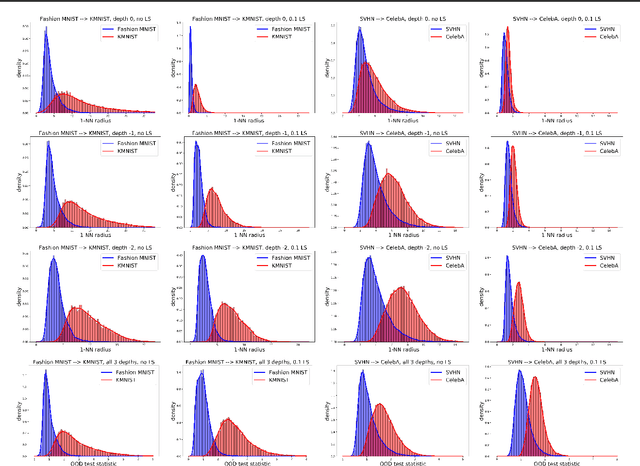



Detecting out-of-distribution (OOD) examples is critical in many applications. We propose an unsupervised method to detect OOD samples using a $k$-NN density estimate with respect to a classification model's intermediate activations on in-distribution samples. We leverage a recent insight about label smoothing, which we call the \emph{Label Smoothed Embedding Hypothesis}, and show that one of the implications is that the $k$-NN density estimator performs better as an OOD detection method both theoretically and empirically when the model is trained with label smoothing. Finally, we show that our proposal outperforms many OOD baselines and also provide new finite-sample high-probability statistical results for $k$-NN density estimation's ability to detect OOD examples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge