Label Propagation across Graphs: Node Classification using Graph Neural Tangent Kernels
Paper and Code
Oct 07, 2021
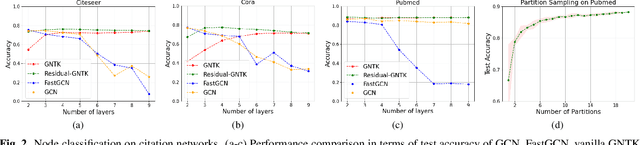
Graph neural networks (GNNs) have achieved superior performance on node classification tasks in the last few years. Commonly, this is framed in a transductive semi-supervised learning setup wherein the entire graph, including the target nodes to be labeled, is available for training. Driven in part by scalability, recent works have focused on the inductive case where only the labeled portion of a graph is available for training. In this context, our current work considers a challenging inductive setting where a set of labeled graphs are available for training while the unlabeled target graph is completely separate, i.e., there are no connections between labeled and unlabeled nodes. Under the implicit assumption that the testing and training graphs come from similar distributions, our goal is to develop a labeling function that generalizes to unobserved connectivity structures. To that end, we employ a graph neural tangent kernel (GNTK) that corresponds to infinitely wide GNNs to find correspondences between nodes in different graphs based on both the topology and the node features. We augment the capabilities of the GNTK with residual connections and empirically illustrate its performance gains on standard benchmarks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge