Kernel Mean Embedding of Instance-wise Predictions in Multiple Instance Regression
Paper and Code
Apr 24, 2019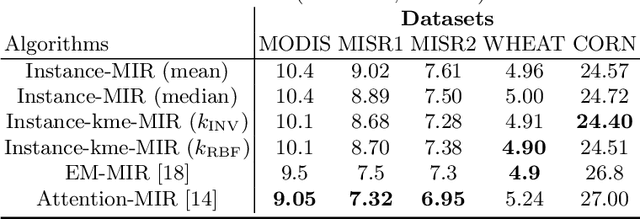
In this paper, we propose an extension to an existing algorithm (instance-MIR) which tackles the multiple instance regression (MIR) problem, also known as distribution regression. The MIR setting arises when the data is a collection of bags, where each bag consists of several instances which correspond to the same and unique real-valued label. The goal of a MIR algorithm is to find a mapping from the instances of an unseen bag to its target value. The instance-MIR algorithm treats all the instances separately and maps each instance to a label. The final bag label is then taken as the mean or the median of the predictions for that given bag. While it is conceptually simple, taking a single statistic to summarize the distribution of the labels in each bag is a limitation. In spite of this performance bottleneck, the instance-MIR algorithm has been shown to be competitive when compared to the current state-of-the-art methods. We address the aforementioned issue by computing the kernel mean embeddings of the distributions of the predicted labels, for each bag, and learn a regressor from these embeddings to the bag label. We test our algorithm (instance-kme-MIR) on five real world datasets and obtain better results than the baseline instance-MIR across all the datasets, while achieving state-of-the-art results on two of the datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge