Kernel Additive Principal Components
Paper and Code
Nov 21, 2015
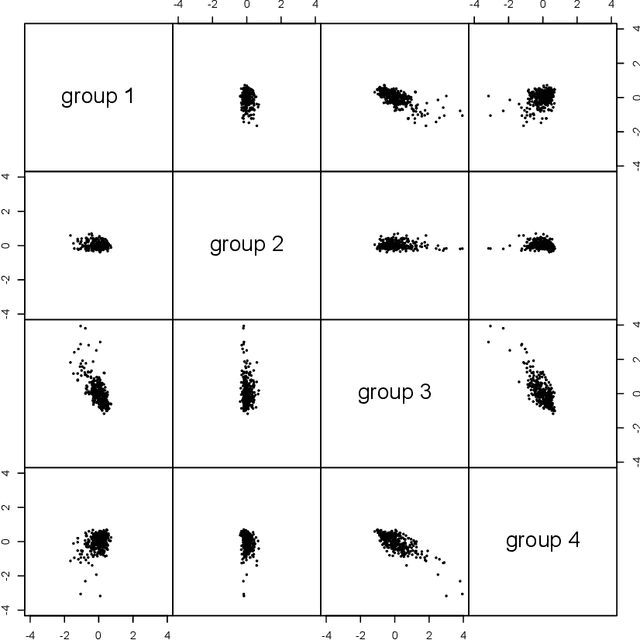
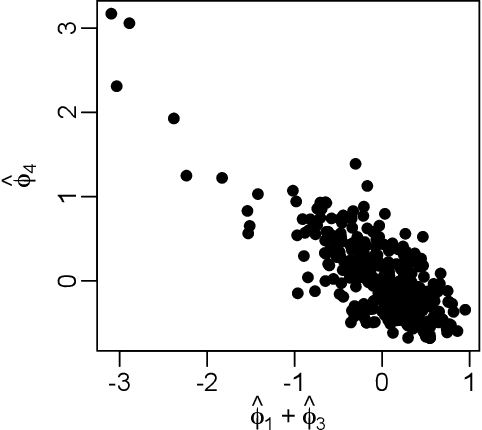
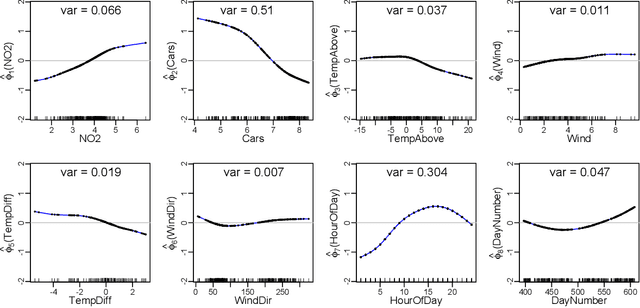
Additive principal components (APCs for short) are a nonlinear generalization of linear principal components. We focus on smallest APCs to describe additive nonlinear constraints that are approximately satisfied by the data. Thus APCs fit data with implicit equations that treat the variables symmetrically, as opposed to regression analyses which fit data with explicit equations that treat the data asymmetrically by singling out a response variable. We propose a regularized data-analytic procedure for APC estimation using kernel methods. In contrast to existing approaches to APCs that are based on regularization through subspace restriction, kernel methods achieve regularization through shrinkage and therefore grant distinctive flexibility in APC estimation by allowing the use of infinite-dimensional functions spaces for searching APC transformation while retaining computational feasibility. To connect population APCs and kernelized finite-sample APCs, we study kernelized population APCs and their associated eigenproblems, which eventually lead to the establishment of consistency of the estimated APCs. Lastly, we discuss an iterative algorithm for computing kernelized finite-sample APCs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge