KAN based Autoencoders for Factor Models

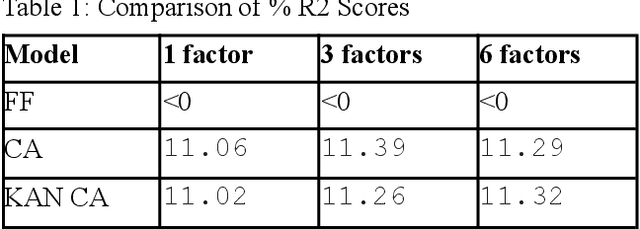
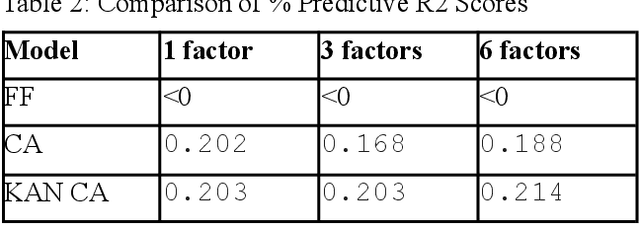
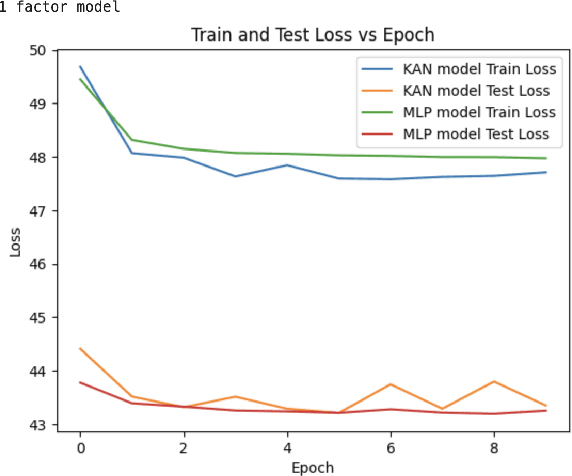
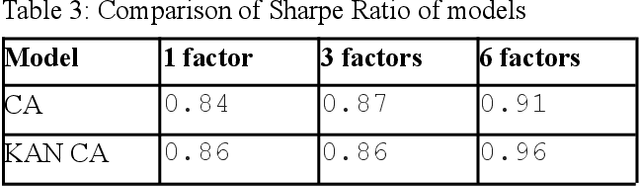
Inspired by recent advances in Kolmogorov-Arnold Networks (KANs), we introduce a novel approach to latent factor conditional asset pricing models. While previous machine learning applications in asset pricing have predominantly used Multilayer Perceptrons with ReLU activation functions to model latent factor exposures, our method introduces a KAN-based autoencoder which surpasses MLP models in both accuracy and interpretability. Our model offers enhanced flexibility in approximating exposures as nonlinear functions of asset characteristics, while simultaneously providing users with an intuitive framework for interpreting latent factors. Empirical backtesting demonstrates our model's superior ability to explain cross-sectional risk exposures. Moreover, long-short portfolios constructed using our model's predictions achieve higher Sharpe ratios, highlighting its practical value in investment management.