$k$-Median Clustering via Metric Embedding: Towards Better Initialization with Differential Privacy
Paper and Code
Jun 26, 2022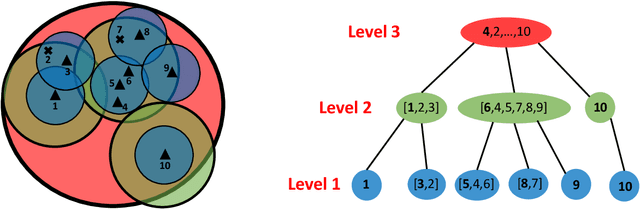
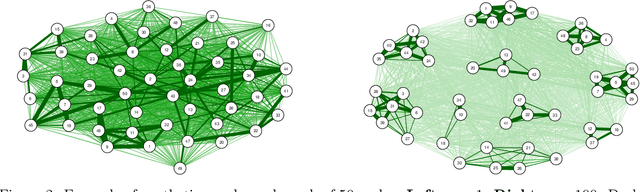
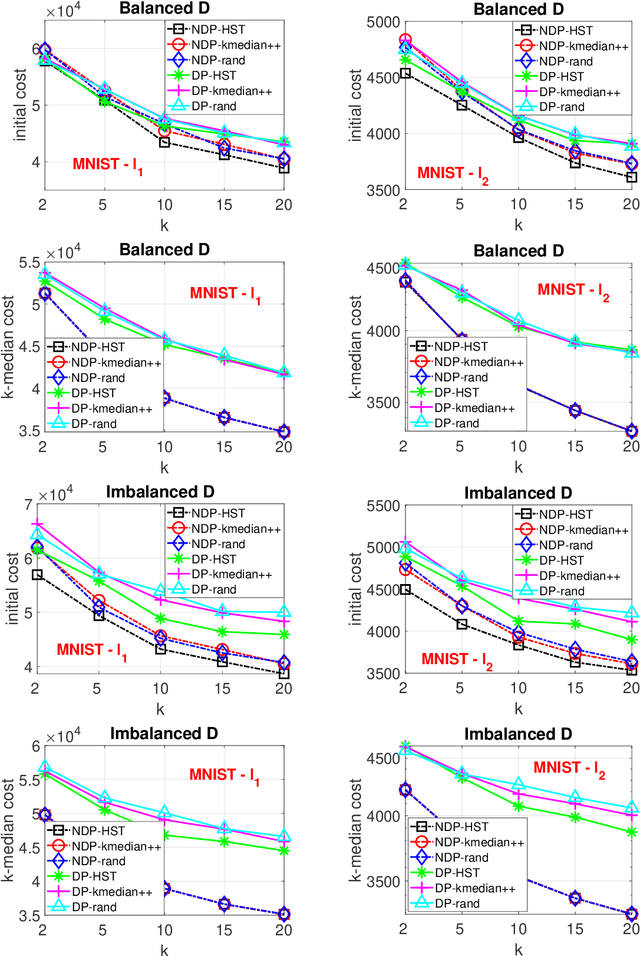
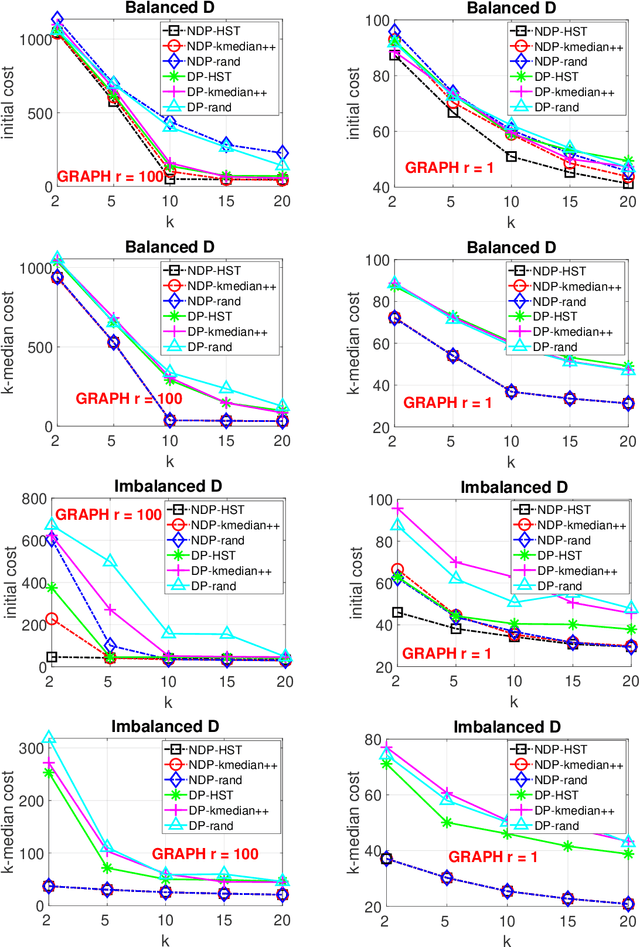
When designing clustering algorithms, the choice of initial centers is crucial for the quality of the learned clusters. In this paper, we develop a new initialization scheme, called HST initialization, for the $k$-median problem in the general metric space (e.g., discrete space induced by graphs), based on the construction of metric embedding tree structure of the data. From the tree, we propose a novel and efficient search algorithm, for good initial centers that can be used subsequently for the local search algorithm. Our proposed HST initialization can produce initial centers achieving lower errors than those from another popular initialization method, $k$-median++, with comparable efficiency. The HST initialization can also be extended to the setting of differential privacy (DP) to generate private initial centers. We show that the error from applying DP local search followed by our private HST initialization improves previous results on the approximation error, and approaches the lower bound within a small factor. Experiments justify the theory and demonstrate the effectiveness of our proposed method. Our approach can also be extended to the $k$-means problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge