k* Distribution: Evaluating the Latent Space of Deep Neural Networks using Local Neighborhood Analysis
Paper and Code
Dec 07, 2023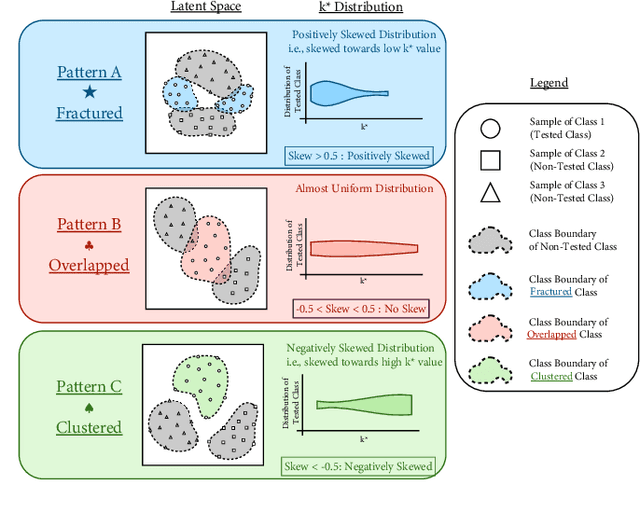

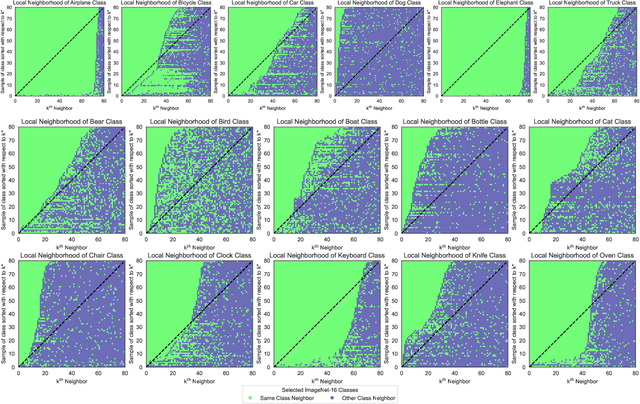

Most examinations of neural networks' learned latent spaces typically employ dimensionality reduction techniques such as t-SNE or UMAP. While these methods effectively capture the overall sample distribution in the entire learned latent space, they tend to distort the structure of sample distributions within specific classes in the subset of the latent space. This distortion complicates the task of easily distinguishing classes identifiable by neural networks. In response to this challenge, we introduce the k* Distribution methodology. This approach focuses on capturing the characteristics and structure of sample distributions for individual classes within the subset of the learned latent space using local neighborhood analysis. The key concept is to facilitate easy comparison of different k* distributions, enabling analysis of how various classes are processed by the same neural network. This provides a more profound understanding of existing contemporary visualizations. Our study reveals three distinct distributions of samples within the learned latent space subset: a) Fractured, b) Overlapped, and c) Clustered. We note and demonstrate that the distribution of samples within the network's learned latent space significantly varies depending on the class. Furthermore, we illustrate that our analysis can be applied to explore the latent space of diverse neural network architectures, various layers within neural networks, transformations applied to input samples, and the distribution of training and testing data for neural networks. We anticipate that our approach will facilitate more targeted investigations into neural networks by collectively examining the distribution of different samples within the learned latent space.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge