Joint Modelling of Quantum and Classical Noise over Unity Quantum Channel
Paper and Code
Jun 08, 2022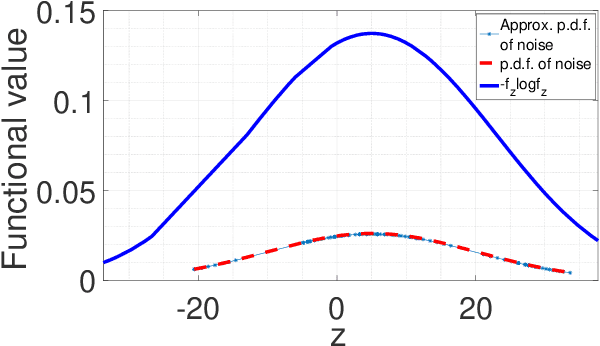
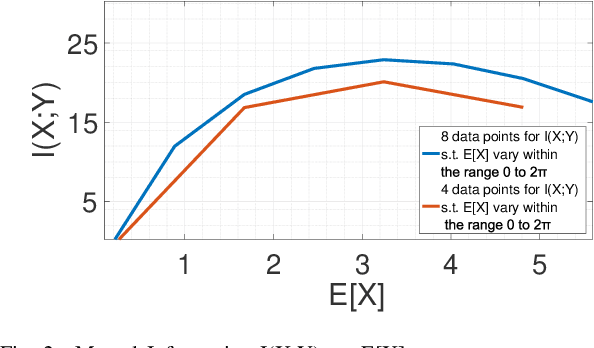
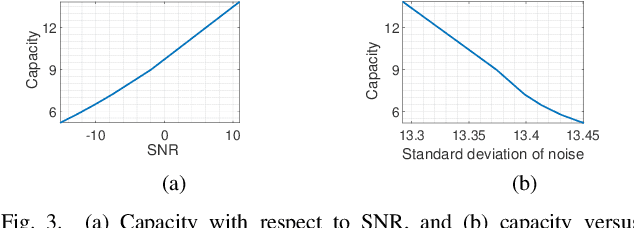
For a continuous-input-continuous-output arbitrarily distributed quantum channel carrying classical information, the channel capacity can be computed in terms of the distribution of the channel envelope, received signal strength over a quantum propagation field and the noise spectral density. If the channel envelope is considered to be unity with unit received signal strength, the factor controlling the capacity is the noise. Quantum channel carrying classical information will suffer from the combination of classical and quantum noise. Assuming additive Gaussian-distributed classical noise and Poisson-distributed quantum noise, we formulate a hybrid noise model by deriving a joint Gaussian- Poisson distribution in this letter. For the transmitted signal, we consider the mean of signal sample space instead of considering a particular distribution and study how the maximum mutual information varies over such mean value. Capacity is estimated by maximizing the mutual information over unity channel envelope.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge