Iterative Hierarchical Optimization for Misspecified Problems (IHOMP)
Paper and Code
Jun 07, 2016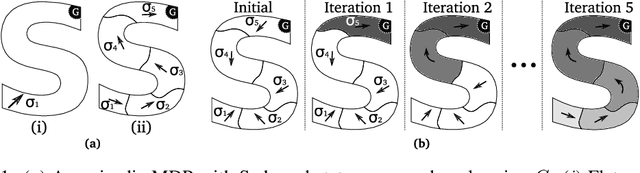
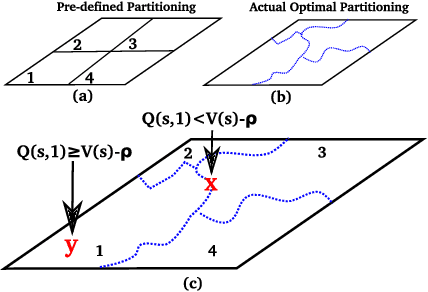

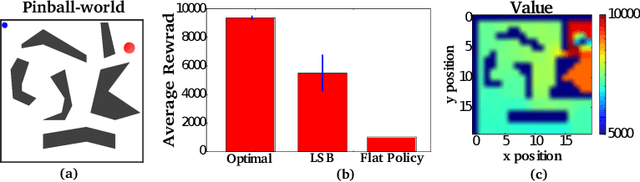
For complex, high-dimensional Markov Decision Processes (MDPs), it may be necessary to represent the policy with function approximation. A problem is misspecified whenever, the representation cannot express any policy with acceptable performance. We introduce IHOMP : an approach for solving misspecified problems. IHOMP iteratively learns a set of context specialized options and combines these options to solve an otherwise misspecified problem. Our main contribution is proving that IHOMP enjoys theoretical convergence guarantees. In addition, we extend IHOMP to exploit Option Interruption (OI) enabling it to decide where the learned options can be reused. Our experiments demonstrate that IHOMP can find near-optimal solutions to otherwise misspecified problems and that OI can further improve the solutions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge