It Ain't That Bad: Understanding the Mysterious Performance Drop in OOD Generalization for Generative Transformer Models
Paper and Code
Aug 16, 2023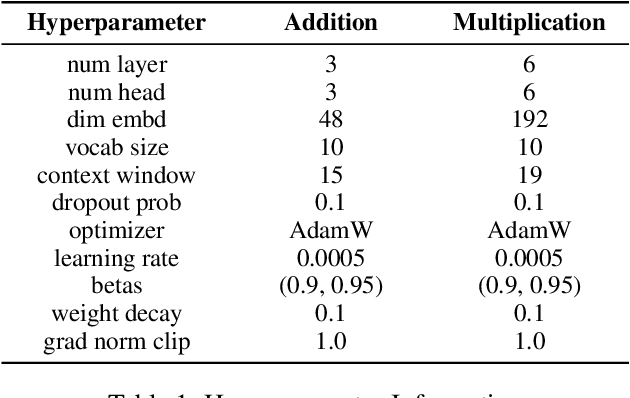
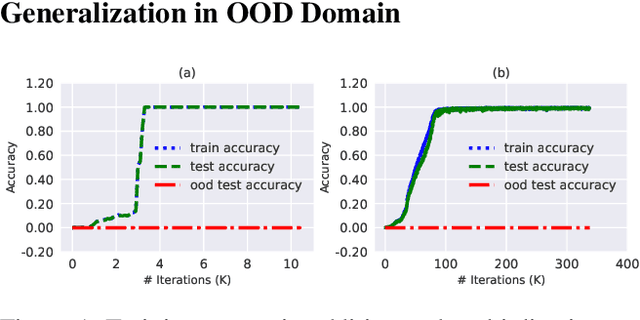
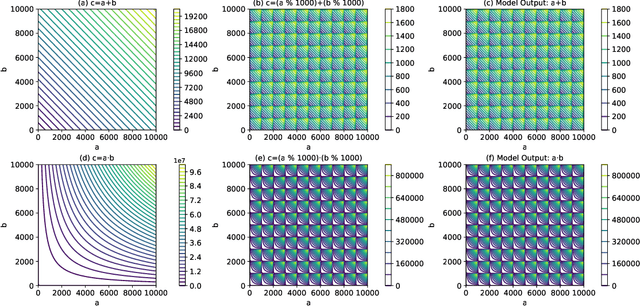
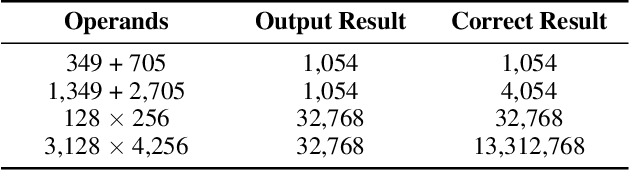
Generative Transformer-based models have achieved remarkable proficiency on solving diverse problems. However, their generalization ability is not fully understood and not always satisfying. Researchers take basic mathematical tasks like n-digit addition or multiplication as important perspectives for investigating their generalization behaviors. Curiously, it is observed that when training on n-digit operations (e.g., additions) in which both input operands are n-digit in length, models generalize successfully on unseen n-digit inputs (in-distribution (ID) generalization), but fail miserably and mysteriously on longer, unseen cases (out-of-distribution (OOD) generalization). Studies try to bridge this gap with workarounds such as modifying position embedding, fine-tuning, and priming with more extensive or instructive data. However, without addressing the essential mechanism, there is hardly any guarantee regarding the robustness of these solutions. We bring this unexplained performance drop into attention and ask whether it is purely from random errors. Here we turn to the mechanistic line of research which has notable successes in model interpretability. We discover that the strong ID generalization stems from structured representations, while behind the unsatisfying OOD performance, the models still exhibit clear learned algebraic structures. Specifically, these models map unseen OOD inputs to outputs with equivalence relations in the ID domain. These highlight the potential of the models to carry useful information for improved generalization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge