IsoScore: Measuring the Uniformity of Vector Space Utilization

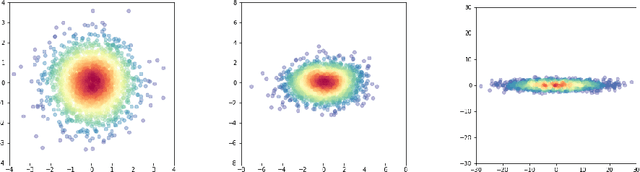
The recent success of distributed word representations has led to an increased interest in analyzing the properties of their spatial distribution. Current metrics suggest that contextualized word embedding models do not uniformly utilize all dimensions when embedding tokens in vector space. Here we argue that existing metrics are fragile and tend to obfuscate the true spatial distribution of point clouds. To ameliorate this issue, we propose IsoScore: a novel metric which quantifies the degree to which a point cloud uniformly utilizes the ambient vector space. We demonstrate that IsoScore has several desirable properties such as mean invariance and direct correspondence to the number of dimensions used, which are properties that existing scores do not possess. Furthermore, IsoScore is conceptually intuitive and computationally efficient, making it well suited for analyzing the distribution of point clouds in arbitrary vector spaces, not necessarily limited to those of word embeddings alone. Additionally, we use IsoScore to demonstrate that a number of recent conclusions in the NLP literature that have been derived using brittle metrics of spatial distribution, such as average cosine similarity, may be incomplete or altogether inaccurate.