Is Batch Norm unique? An empirical investigation and prescription to emulate the best properties of common normalizers without batch dependence
Paper and Code
Oct 21, 2020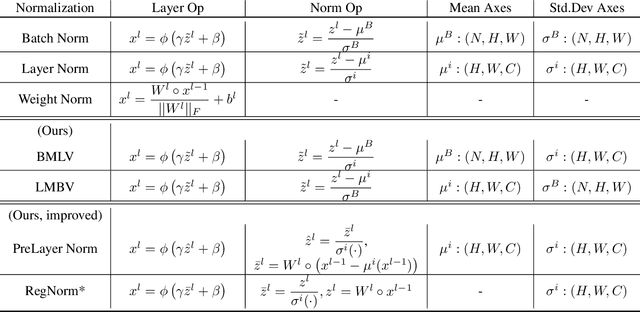
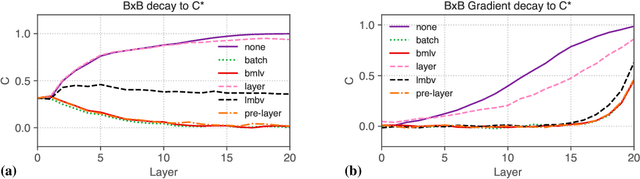
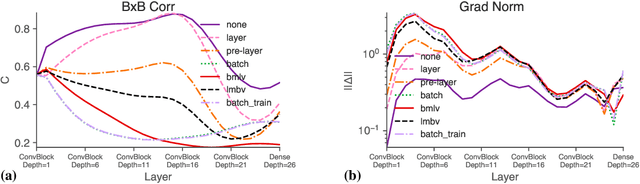
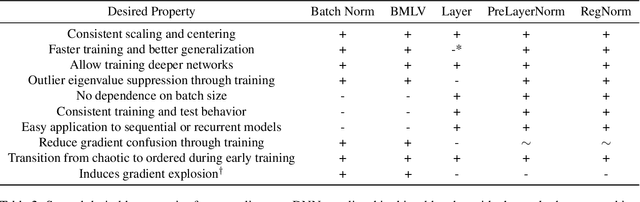
We perform an extensive empirical study of the statistical properties of Batch Norm and other common normalizers. This includes an examination of the correlation between representations of minibatches, gradient norms, and Hessian spectra both at initialization and over the course of training. Through this analysis, we identify several statistical properties which appear linked to Batch Norm's superior performance. We propose two simple normalizers, PreLayerNorm and RegNorm, which better match these desirable properties without involving operations along the batch dimension. We show that PreLayerNorm and RegNorm achieve much of the performance of Batch Norm without requiring batch dependence, that they reliably outperform LayerNorm, and that they can be applied in situations where Batch Norm is ineffective.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge