Inverting brain grey matter models with likelihood-free inference: a tool for trustable cytoarchitecture measurements
Paper and Code
Nov 15, 2021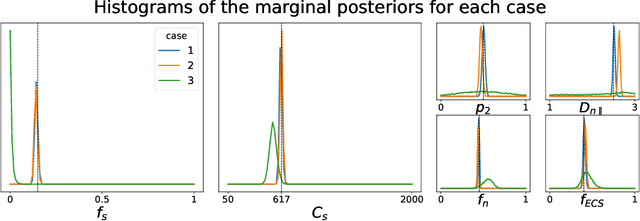
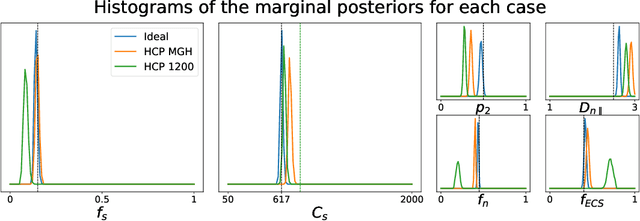
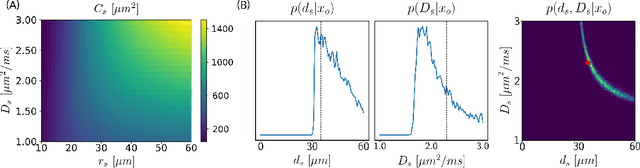
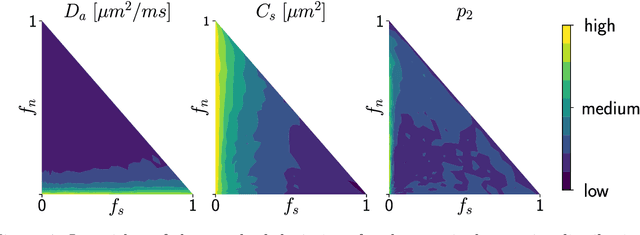
Effective characterisation of the brain grey matter cytoarchitecture with quantitative sensitivity to soma density and volume remains an unsolved challenge in diffusion MRI (dMRI). Solving the problem of relating the dMRI signal with cytoarchitectural characteristics calls for the definition of a mathematical model that describes brain tissue via a handful of physiologically-relevant parameters and an algorithm for inverting the model. To address this issue, we propose a new forward model, specifically a new system of equations, requiring a few relatively sparse b-shells. We then apply modern tools from Bayesian analysis known as likelihood-free inference (LFI) to invert our proposed model. As opposed to other approaches from the literature, our algorithm yields not only an estimation of the parameter vector $\theta$ that best describes a given observed data point $x_0$, but also a full posterior distribution $p(\theta|x_0)$ over the parameter space. This enables a richer description of the model inversion, providing indicators such as credible intervals for the estimated parameters and a complete characterization of the parameter regions where the model may present indeterminacies. We approximate the posterior distribution using deep neural density estimators, known as normalizing flows, and fit them using a set of repeated simulations from the forward model. We validate our approach on simulations using dmipy and then apply the whole pipeline on two publicly available datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge