Inverse Kinematics for Control of Tensegrity Soft Robots: Existence and Optimality of Solutions

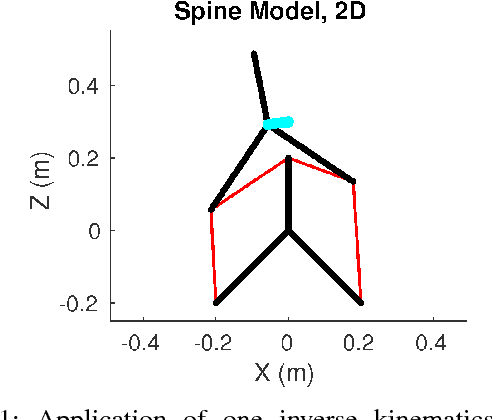
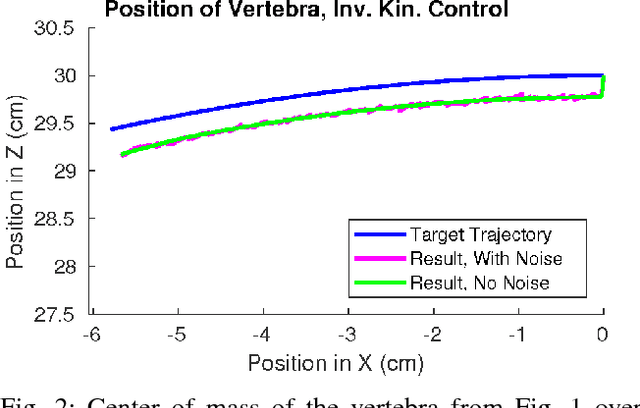
Tension-network (`tensegrity') robots encounter many control challenges as articulated soft robots, due to the structures' high-dimensional nonlinear dynamics. Control approaches have been developed which use the inverse kinematics of tensegrity structures, either for open-loop control or as equilibrium inputs for closed-loop controllers. However, current formulations of the tensegrity inverse kinematics problem are limited in robotics applications: first, they can lead to higher than needed cable tensions, and second, may lack solutions when applied to robots with high node-to-cable ratios. This work provides progress in both directions. To address the first limitation, the objective function for the inverse kinematics optimization problem is modified to produce cable tensions as low or lower than before, thus reducing the load on the robots' motors. For the second, a reformulation of the static equilibrium constraint is proposed, which produces solutions independent of the number of nodes within each rigid body. Simulation results using the second reformulation on a specific tensegrity spine robot show reasonable open-loop control results, whereas the previous formulation could not produce any solution.