Introducing a Calculus of Effects and Handlers for Natural Language Semantics
Paper and Code
Jul 08, 2016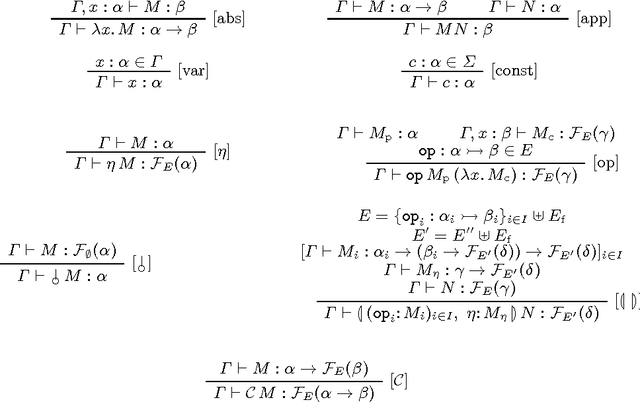
In compositional model-theoretic semantics, researchers assemble truth-conditions or other kinds of denotations using the lambda calculus. It was previously observed that the lambda terms and/or the denotations studied tend to follow the same pattern: they are instances of a monad. In this paper, we present an extension of the simply-typed lambda calculus that exploits this uniformity using the recently discovered technique of effect handlers. We prove that our calculus exhibits some of the key formal properties of the lambda calculus and we use it to construct a modular semantics for a small fragment that involves multiple distinct semantic phenomena.
* Formal Grammar 2016, Aug 2016, Bozen-Bolzano, Italy
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge