Intriguing Properties of Contrastive Losses
Paper and Code
Nov 05, 2020

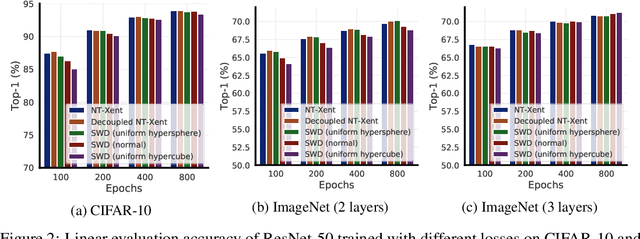
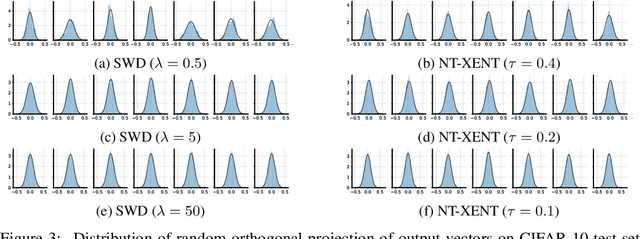
Contrastive loss and its variants have become very popular recently for learning visual representations without supervision. In this work, we first generalize the standard contrastive loss based on cross entropy to a broader family of losses that share an abstract form of $\mathcal{L}_{\text{alignment}} + \lambda \mathcal{L}_{\text{distribution}}$, where hidden representations are encouraged to (1) be aligned under some transformations/augmentations, and (2) match a prior distribution of high entropy. We show that various instantiations of the generalized loss perform similarly under the presence of a multi-layer non-linear projection head, and the temperature scaling ($\tau$) widely used in the standard contrastive loss is (within a range) inversely related to the weighting ($\lambda$) between the two loss terms. We then study an intriguing phenomenon of feature suppression among competing features shared acros augmented views, such as "color distribution" vs "object class". We construct datasets with explicit and controllable competing features, and show that, for contrastive learning, a few bits of easy-to-learn shared features could suppress, and even fully prevent, the learning of other sets of competing features. Interestingly, this characteristic is much less detrimental in autoencoders based on a reconstruction loss. Existing contrastive learning methods critically rely on data augmentation to favor certain sets of features than others, while one may wish that a network would learn all competing features as much as its capacity allows.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge