Interpolation, extrapolation, and local generalization in common neural networks

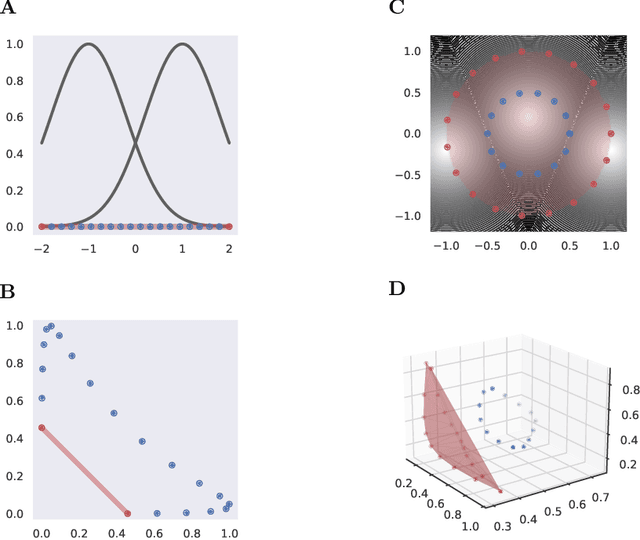
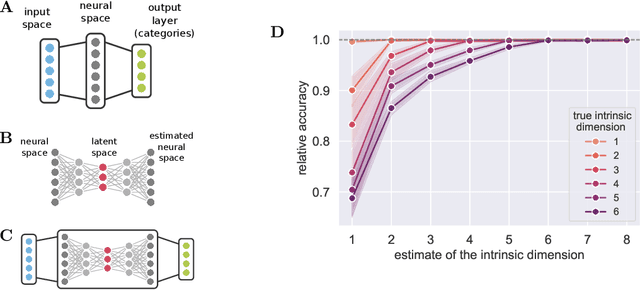
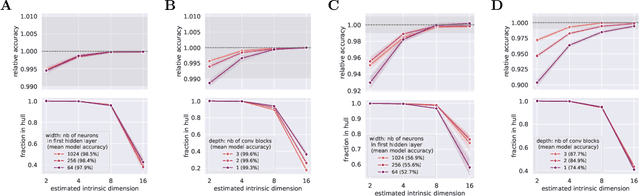
There has been a long history of works showing that neural networks have hard time extrapolating beyond the training set. A recent study by Balestriero et al. (2021) challenges this view: defining interpolation as the state of belonging to the convex hull of the training set, they show that the test set, either in input or neural space, cannot lie for the most part in this convex hull, due to the high dimensionality of the data, invoking the well known curse of dimensionality. Neural networks are then assumed to necessarily work in extrapolative mode. We here study the neural activities of the last hidden layer of typical neural networks. Using an autoencoder to uncover the intrinsic space underlying the neural activities, we show that this space is actually low-dimensional, and that the better the model, the lower the dimensionality of this intrinsic space. In this space, most samples of the test set actually lie in the convex hull of the training set: under the convex hull definition, the models thus happen to work in interpolation regime. Moreover, we show that belonging to the convex hull does not seem to be the relevant criteria. Different measures of proximity to the training set are actually better related to performance accuracy. Thus, typical neural networks do seem to operate in interpolation regime. Good generalization performances are linked to the ability of a neural network to operate well in such a regime.