Integrable Nonparametric Flows
Paper and Code
Dec 03, 2020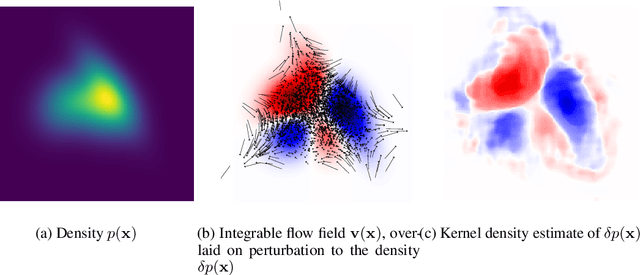
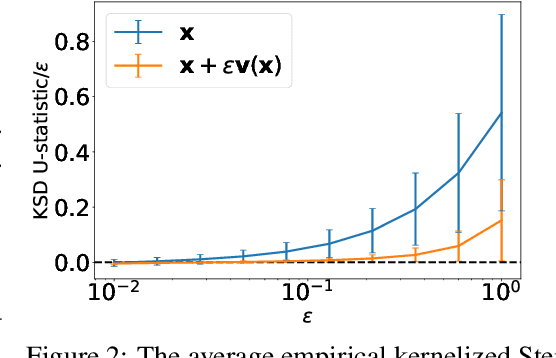
We introduce a method for reconstructing an infinitesimal normalizing flow given only an infinitesimal change to a (possibly unnormalized) probability distribution. This reverses the conventional task of normalizing flows -- rather than being given samples from a unknown target distribution and learning a flow that approximates the distribution, we are given a perturbation to an initial distribution and aim to reconstruct a flow that would generate samples from the known perturbed distribution. While this is an underdetermined problem, we find that choosing the flow to be an integrable vector field yields a solution closely related to electrostatics, and a solution can be computed by the method of Green's functions. Unlike conventional normalizing flows, this flow can be represented in an entirely nonparametric manner. We validate this derivation on low-dimensional problems, and discuss potential applications to problems in quantum Monte Carlo and machine learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge