Input-sensitive dense-sparse primitive compositions for GNN acceleration
Paper and Code
Jun 27, 2023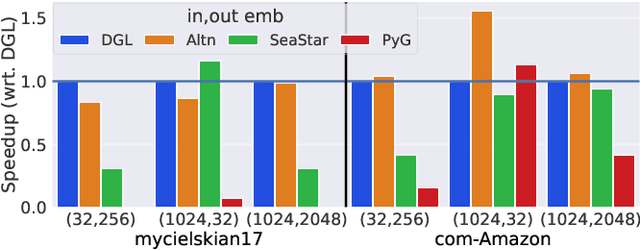
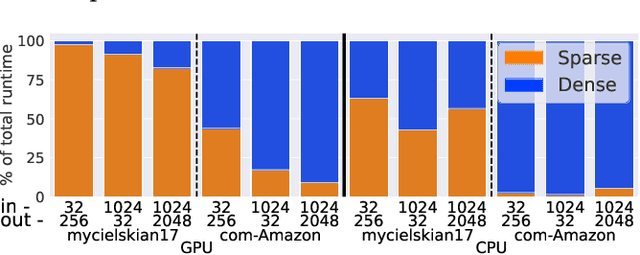
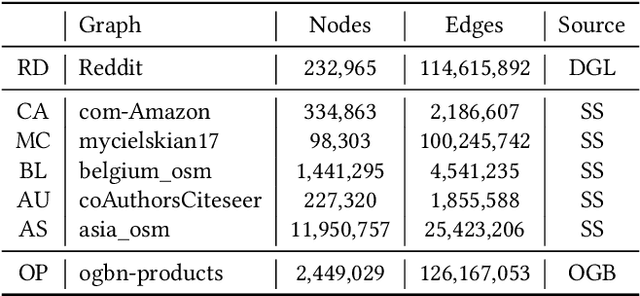
Graph neural networks (GNN) have become an important class of neural network models that have gained popularity in domains such as social and financial network analysis. Different phases of GNN computations can be modeled using both dense and sparse matrix operations. There have been many frameworks and optimization techniques proposed in the literature to accelerate GNNs. However, getting consistently high performance across many input graphs with different sparsity patterns and GNN embedding sizes has remained difficult. In this paper, we propose different algebraic reassociations of GNN computations that lead to novel dense and sparse matrix primitive selections and compositions. We show that the profitability of these compositions depends on the input graph, embedding size, and the target hardware. We developed SENSEi, a system that uses a data-driven adaptive strategy to select the best composition given the input graph and GNN embedding sizes. Our evaluations on a wide range of graphs and embedding sizes show that SENSEi achieves geomean speedups of $1.105\times$ (up to $2.959\times$) and $1.187\times$ (up to $1.99\times$) on graph convolutional networks and geomean speedups of $2.307\times$ (up to $35.866\times$) and $1.44\times$ (up to $5.69\times$) on graph attention networks on CPUs and GPUs respectively over the widely used Deep Graph Library. Further, we show that the compositions yield notable synergistic performance benefits on top of other established sparse optimizations such as sparse matrix tiling by evaluating against a well-tuned baseline.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge