Inherent Noise in Gradient Based Methods
Paper and Code
May 26, 2020

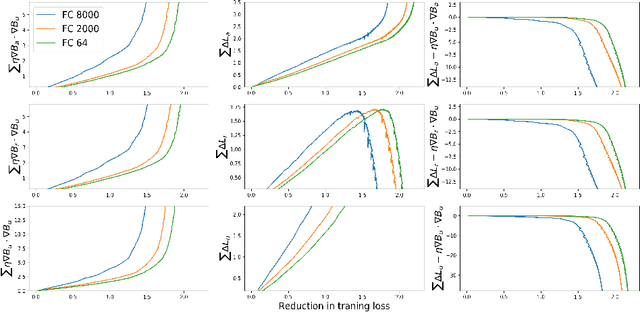

Previous work has examined the ability of larger capacity neural networks to generalize better than smaller ones, even without explicit regularizers, by analyzing gradient based algorithms such as GD and SGD. The presence of noise and its effect on robustness to parameter perturbations has been linked to generalization. We examine a property of GD and SGD, namely that instead of iterating through all scalar weights in the network and updating them one by one, GD (and SGD) updates all the parameters at the same time. As a result, each parameter $w^i$ calculates its partial derivative at the stale parameter $\mathbf{w_t}$, but then suffers loss $\hat{L}(\mathbf{w_{t+1}})$. We show that this causes noise to be introduced into the optimization. We find that this noise penalizes models that are sensitive to perturbations in the weights. We find that penalties are most pronounced for batches that are currently being used to update, and are higher for larger models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge