Infinite-dimensional optimization and Bayesian nonparametric learning of stochastic differential equations
Paper and Code
May 30, 2022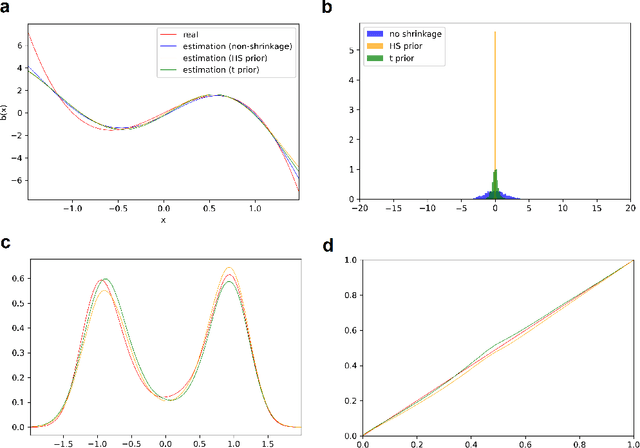



The paper has two major themes. The first part of the paper establishes certain general results for infinite-dimensional optimization problems on Hilbert spaces. These results cover the classical representer theorem and many of its variants as special cases and offer a wider scope of applications. The second part of the paper then develops a systematic approach for learning the drift function of a stochastic differential equation by integrating the results of the first part with Bayesian hierarchical framework. Importantly, our Baysian approach incorporates low-cost sparse learning through proper use of shrinkage priors while allowing proper quantification of uncertainty through posterior distributions. Several examples at the end illustrate the accuracy of our learning scheme.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge