Inferring Global Dynamics Using a Learning Machine
Paper and Code
Sep 28, 2020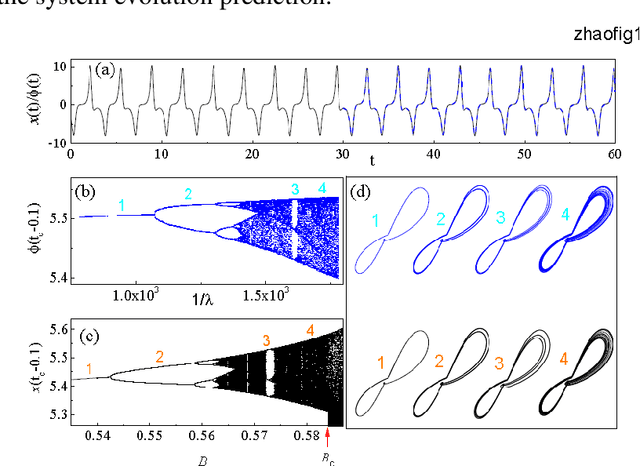
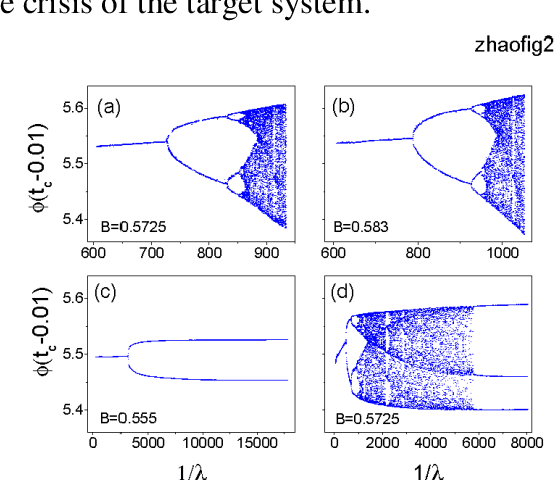
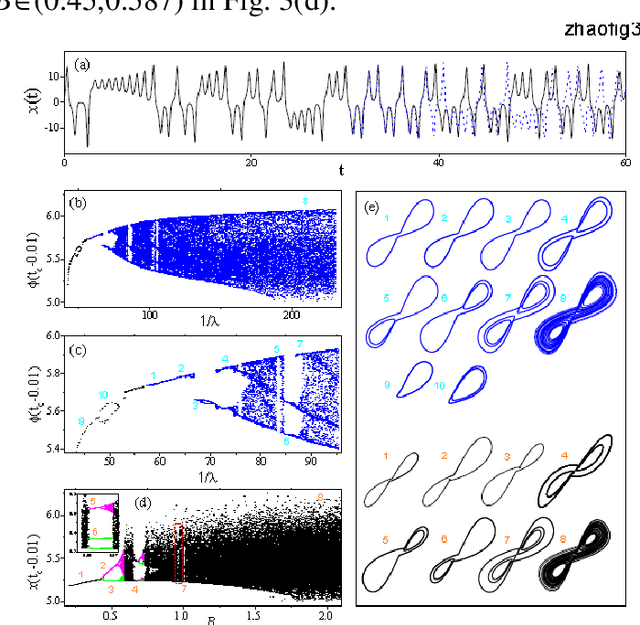
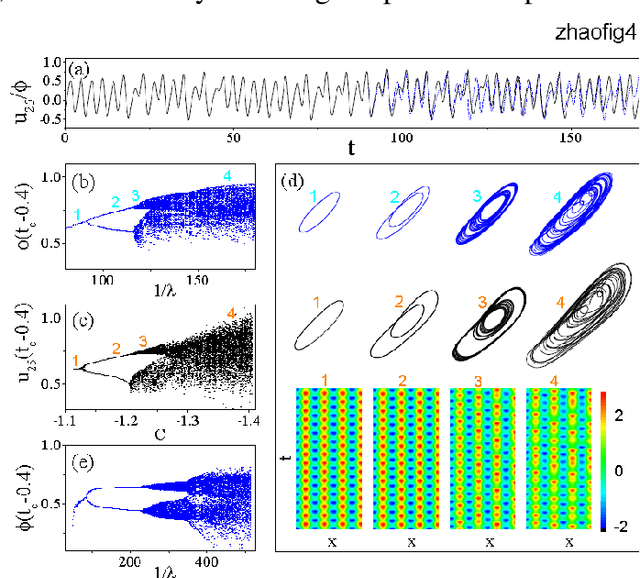
Given a segment of time series of a system at a particular set of parameter values, can one infers the global behavior of the system in its parameter space? Here we show that by using a learning machine we can achieve such a goal to a certain extent. It is found that following an appropriate training strategy that monotonously decreases the cost function, the learning machine in different training stage can mimic the system at different parameter set. Consequently, the global dynamical properties of the system is subsequently revealed, usually in the simple-to-complex order. The underlying mechanism is attributed to the training strategy, which causes the learning machine to collapse to a qualitatively equivalent system of the system behind the time series. Thus, the learning machine opens up a novel way to probe the global dynamical properties of a black-box system without artificially establish the equations of motion. The given illustrating examples include a representative model of low-dimensional nonlinear dynamical systems and a spatiotemporal model of reaction-diffusion systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge