Inadequacy of Linear Methods for Minimal Sensor Placement and Feature Selection in Nonlinear Systems; a New Approach Using Secants
Paper and Code
Jan 27, 2021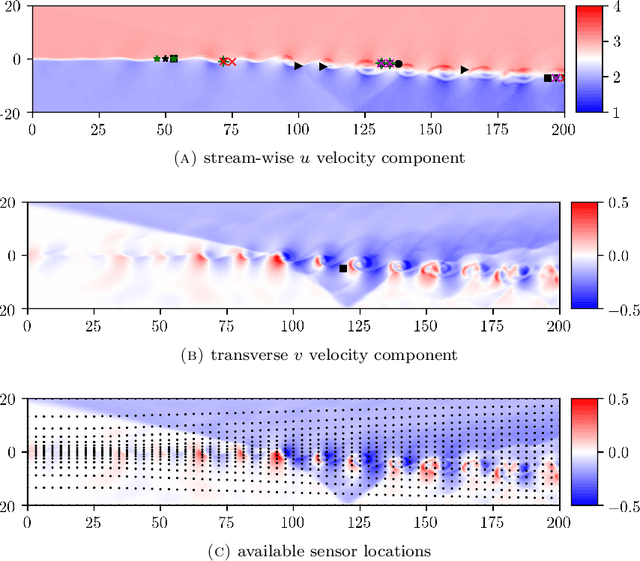

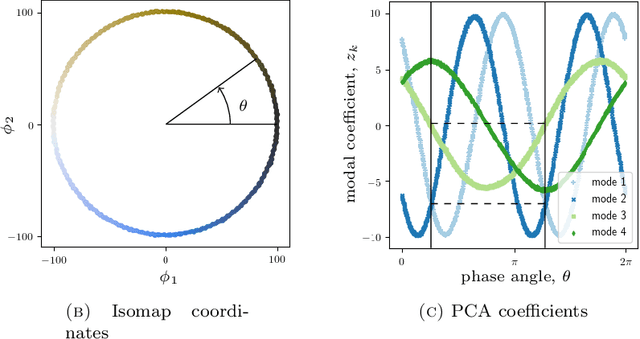
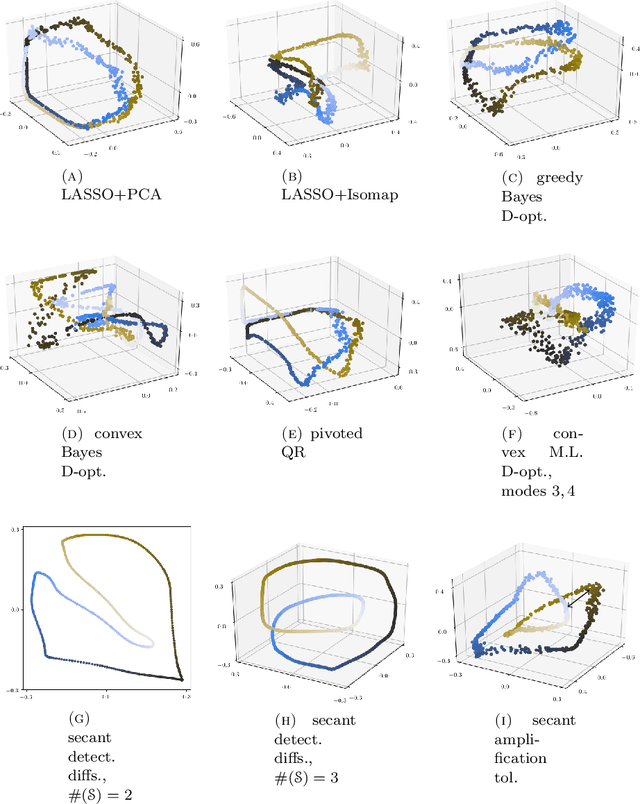
Sensor placement and feature selection are critical steps in engineering, modeling, and data science that share a common mathematical theme: the selected measurements should enable solution of an inverse problem. Most real-world systems of interest are nonlinear, yet the majority of available techniques for feature selection and sensor placement rely on assumptions of linearity or simple statistical models. We show that when these assumptions are violated, standard techniques can lead to costly over-sensing without guaranteeing that the desired information can be recovered from the measurements. In order to remedy these problems, we introduce a novel data-driven approach for sensor placement and feature selection for a general type of nonlinear inverse problem based on the information contained in secant vectors between data points. Using the secant-based approach, we develop three efficient greedy algorithms that each provide different types of robust, near-minimal reconstruction guarantees. We demonstrate them on two problems where linear techniques consistently fail: sensor placement to reconstruct a fluid flow formed by a complicated shock-mixing layer interaction and selecting fundamental manifold learning coordinates on a torus.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge