In Defense of Uniform Convergence: Generalization via derandomization with an application to interpolating predictors

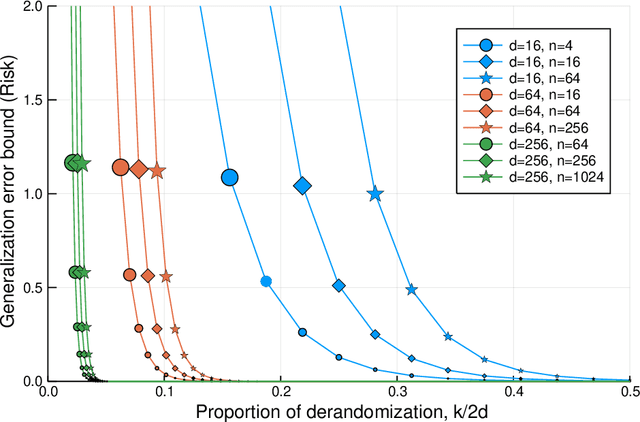
We propose to study the generalization error of a learned predictor $\hat h$ in terms of that of a surrogate (potentially randomized) classifier that is coupled to $\hat h$ and designed to trade empirical risk for control of generalization error. In the case where $\hat h$ interpolates the data, it is interesting to consider theoretical surrogate classifiers that are partially derandomized or rerandomized, e.g., fit to the training data but with modified label noise. We show that replacing $\hat h$ by its conditional distribution with respect to an arbitrary $\sigma$-field is a viable method to derandomize. We give an example, inspired by the work of Nagarajan and Kolter (2019), where the learned classifier $\hat h$ interpolates the training data with high probability, has small risk, and, yet, does not belong to a nonrandom class with a tight uniform bound on two-sided generalization error. At the same time, we bound the risk of $\hat h$ in terms of a surrogate that is constructed by conditioning and shown to belong to a nonrandom class with uniformly small generalization error.