Improving The Performance Of The K-means Algorithm
Paper and Code
May 10, 2020
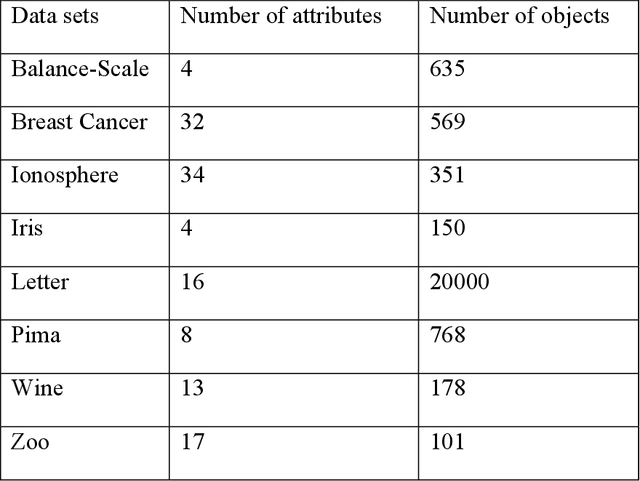

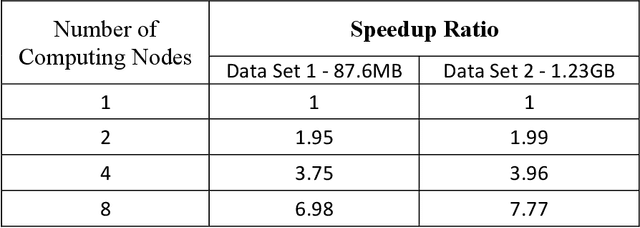
The Incremental K-means (IKM), an improved version of K-means (KM), was introduced to improve the clustering quality of KM significantly. However, the speed of IKM is slower than KM. My thesis proposes two algorithms to speed up IKM while remaining the quality of its clustering result approximately. The first algorithm, called Divisive K-means, improves the speed of IKM by speeding up its splitting process of clusters. Testing with UCI Machine Learning data sets, the new algorithm achieves the empirically global optimum as IKM and has lower complexity, $O(k*log_{2}k*n)$, than IKM, $O(k^{2}n)$. The second algorithm, called Parallel Two-Phase K-means (Par2PK-means), parallelizes IKM by employing the model of Two-Phase K-means. Testing with large data sets, this algorithm attains a good speedup ratio, closing to the linearly speed-up ratio.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge