Improving Regret Bounds for Combinatorial Semi-Bandits with Probabilistically Triggered Arms and Its Applications
Paper and Code
Feb 21, 2018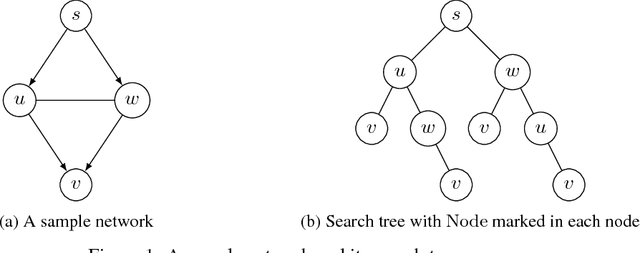
We study combinatorial multi-armed bandit with probabilistically triggered arms (CMAB-T) and semi-bandit feedback. We resolve a serious issue in the prior CMAB-T studies where the regret bounds contain a possibly exponentially large factor of $1/p^*$, where $p^*$ is the minimum positive probability that an arm is triggered by any action. We address this issue by introducing a triggering probability modulated (TPM) bounded smoothness condition into the general CMAB-T framework, and show that many applications such as influence maximization bandit and combinatorial cascading bandit satisfy this TPM condition. As a result, we completely remove the factor of $1/p^*$ from the regret bounds, achieving significantly better regret bounds for influence maximization and cascading bandits than before. Finally, we provide lower bound results showing that the factor $1/p^*$ is unavoidable for general CMAB-T problems, suggesting that the TPM condition is crucial in removing this factor.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge