Improving Bridge estimators via $f$-GAN
Paper and Code
Jun 24, 2021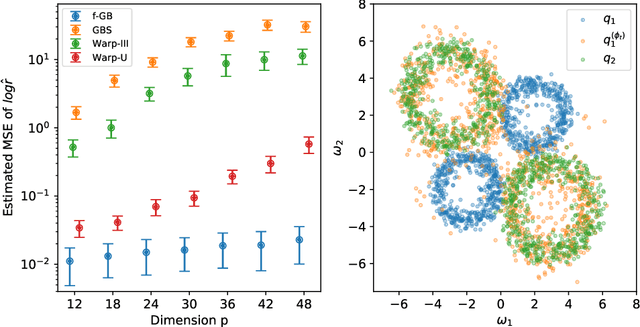
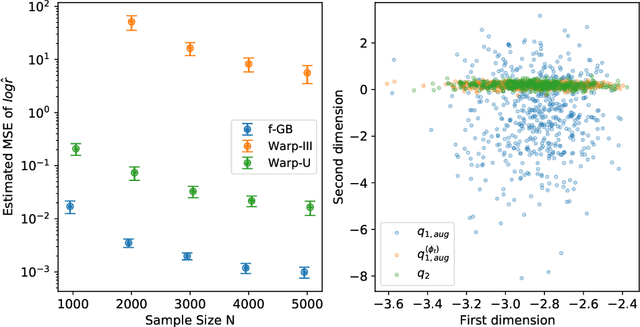

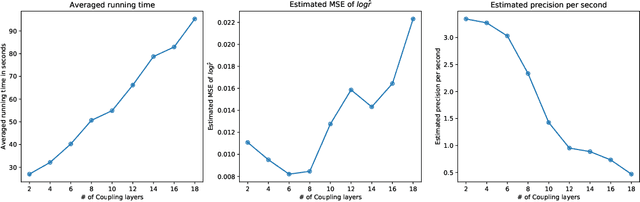
Bridge sampling is a powerful Monte Carlo method for estimating ratios of normalizing constants. Various methods have been introduced to improve its efficiency. These methods aim to increase the overlap between the densities by applying appropriate transformations to them without changing their normalizing constants. In this paper, we first give a new estimator of the asymptotic relative mean square error (RMSE) of the optimal Bridge estimator by equivalently estimating an $f$-divergence between the two densities. We then utilize this framework and propose $f$-GAN-Bridge estimator ($f$-GB) based on a bijective transformation that maps one density to the other and minimizes the asymptotic RMSE of the optimal Bridge estimator with respect to the densities. This transformation is chosen by minimizing a specific $f$-divergence between the densities using an $f$-GAN. We show $f$-GB is optimal in the sense that within any given set of candidate transformations, the $f$-GB estimator can asymptotically achieve an RMSE lower than or equal to that achieved by Bridge estimators based on any other transformed densities. Numerical experiments show that $f$-GB outperforms existing methods in simulated and real-world examples. In addition, we discuss how Bridge estimators naturally arise from the problem of $f$-divergence estimation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge