Improved PCRLB for radar tracking in clutter with geometry-dependent target measurement uncertainty and application to radar trajectory control
Paper and Code
Oct 08, 2024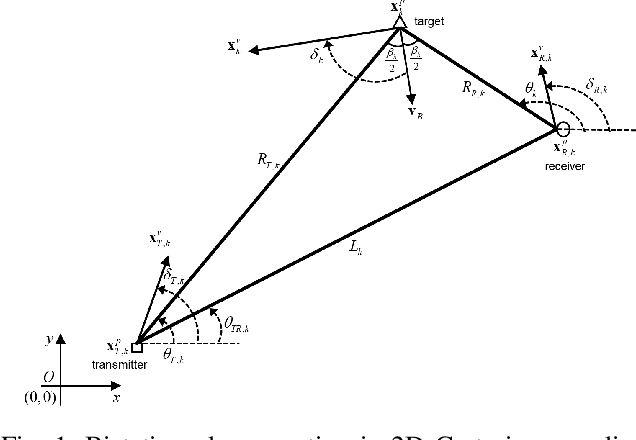
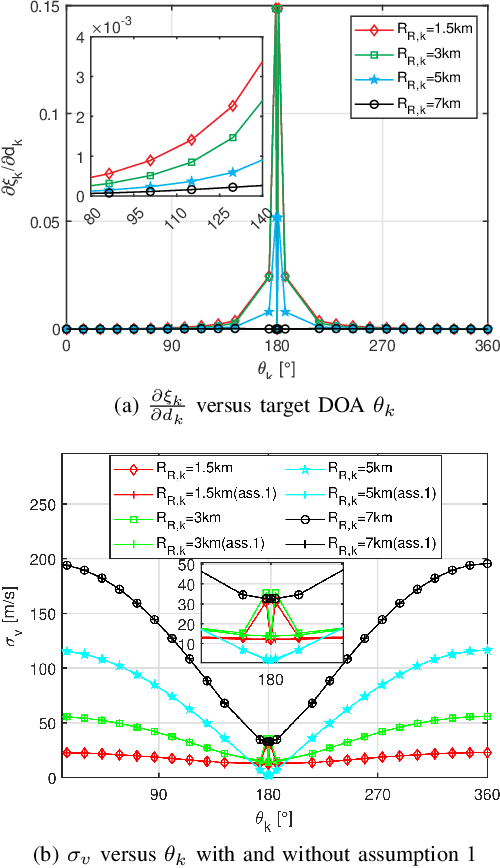
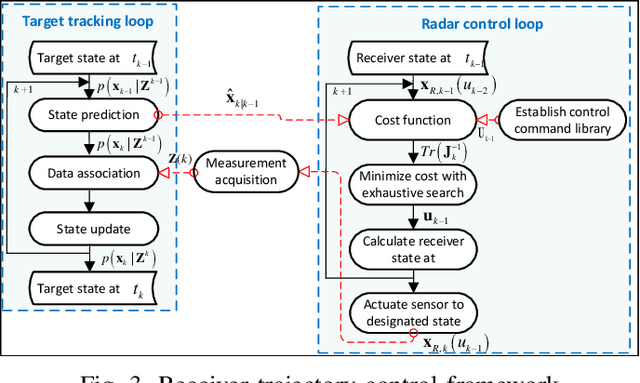
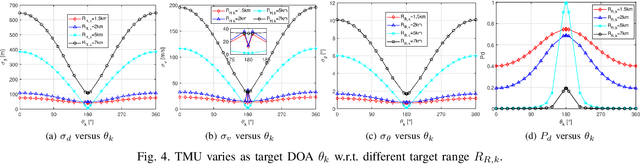
In realistic radar tracking, target measurement uncertainty (TMU) in terms of both detection probability and measurement error covariance is significantly affected by the target-to-radar (T2R) geometry. However, existing posterior Cramer-Rao Lower Bounds (PCRLBs) rarely investigate the fundamental impact of T2R geometry on target measurement uncertainty and eventually on mean square error (MSE) of state estimate, inevitably resulting in over-conservative lower bound. To address this issue, this paper firstly derives the generalized model of target measurement error covariance for bistatic radar with moving receiver and transmitter illuminating any type of signal, along with its approximated solution to specify the impact of T2R geometry on error covariance. Based upon formulated TMU model, an improved PCRLB (IPCRLB) fully accounting for both measurement origin uncertainty and geometry-dependent TMU is then re-derived, both detection probability and measurement error covariance are treated as state-dependent parameters when differentiating log-likelihood with respect to target state. Compared to existing PCRLBs that partially or completely ignore the dependence of target measurement uncertainty on T2R geometry, proposed IPCRLB provides a much accurate (less-conservative) lower bound for radar tracking in clutter with geometry-dependent TMU. The new bound is then applied to radar trajectory control to effectively optimize T2R geometry and exhibits least uncertainty of acquired target measurement and more accurate state estimate for bistatic radar tracking in clutter, compared to state-of-the-art trajectory control methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge