Implicit regularization and solution uniqueness in over-parameterized matrix sensing

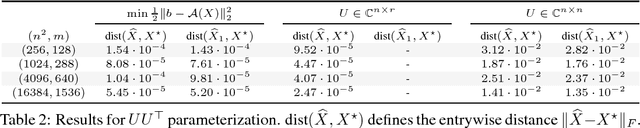
We consider whether algorithmic choices in over-parameterized linear matrix factorization introduce implicit regularization. We focus on noiseless matrix sensing over rank-$r$ positive semi-definite (PSD) matrices in $\mathbb{R}^{n \times n}$, with a sensing mechanism that satisfies the restricted isometry property (RIP). The algorithm we study is that of \emph{factored gradient descent}, where we model the low-rankness and PSD constraints with the factorization $UU^\top$, where $U \in \mathbb{R}^{n \times r}$. Surprisingly, recent work argues that the choice of $r \leq n$ is not pivotal: even setting $U \in \mathbb{R}^{n \times n}$ is sufficient for factored gradient descent to find the rank-$r$ solution, which suggests that operating over the factors leads to an implicit regularization. In this note, we provide a different perspective. We show that, in the noiseless case, under certain conditions, the PSD constraint by itself is sufficient to lead to a unique rank-$r$ matrix recovery, without implicit or explicit low-rank regularization. \emph{I.e.}, under assumptions, the set of PSD matrices, that are consistent with the observed data, is a singleton, irrespective of the algorithm used.