Implicit Generative Prior for Bayesian Neural Networks
Paper and Code
Apr 27, 2024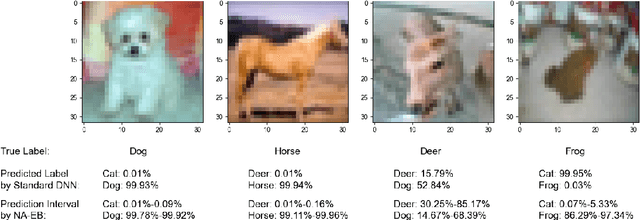
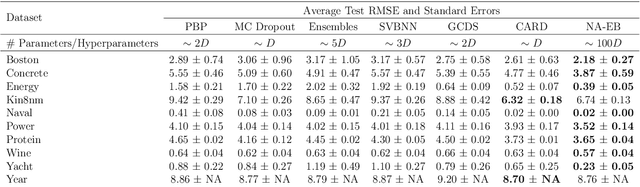
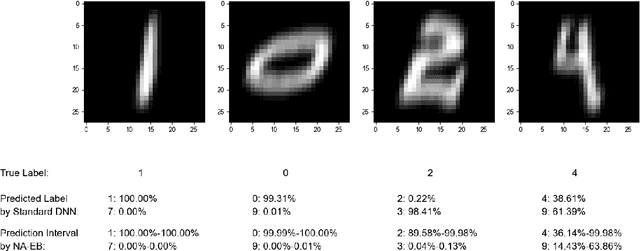
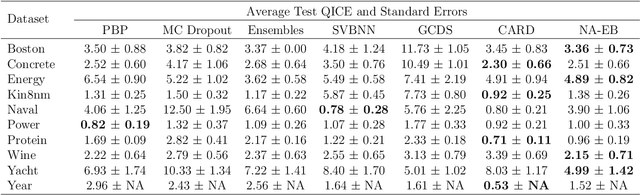
Predictive uncertainty quantification is crucial for reliable decision-making in various applied domains. Bayesian neural networks offer a powerful framework for this task. However, defining meaningful priors and ensuring computational efficiency remain significant challenges, especially for complex real-world applications. This paper addresses these challenges by proposing a novel neural adaptive empirical Bayes (NA-EB) framework. NA-EB leverages a class of implicit generative priors derived from low-dimensional distributions. This allows for efficient handling of complex data structures and effective capture of underlying relationships in real-world datasets. The proposed NA-EB framework combines variational inference with a gradient ascent algorithm. This enables simultaneous hyperparameter selection and approximation of the posterior distribution, leading to improved computational efficiency. We establish the theoretical foundation of the framework through posterior and classification consistency. We demonstrate the practical applications of our framework through extensive evaluations on a variety of tasks, including the two-spiral problem, regression, 10 UCI datasets, and image classification tasks on both MNIST and CIFAR-10 datasets. The results of our experiments highlight the superiority of our proposed framework over existing methods, such as sparse variational Bayesian and generative models, in terms of prediction accuracy and uncertainty quantification.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge