Image classifiers can not be made robust to small perturbations
Paper and Code
Dec 07, 2021
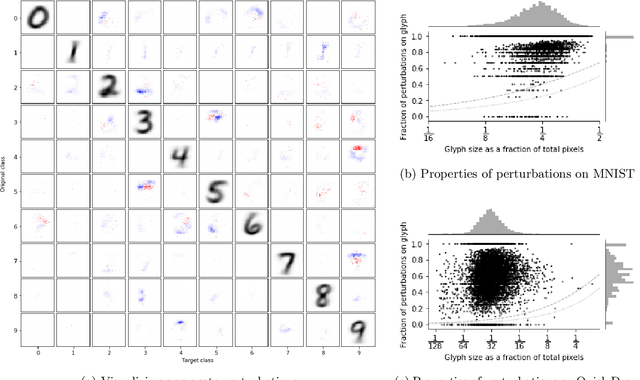
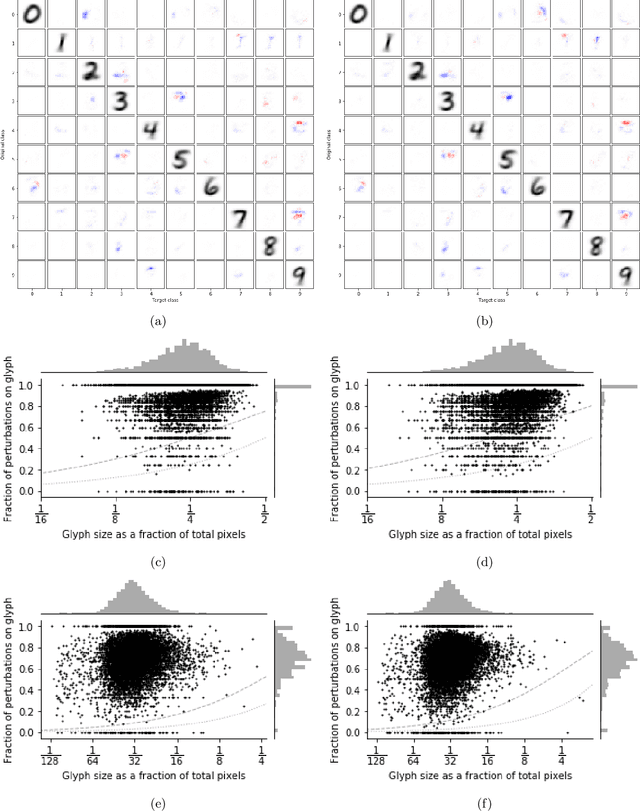
The sensitivity of image classifiers to small perturbations in the input is often viewed as a defect of their construction. We demonstrate that this sensitivity is a fundamental property of classifiers. For any arbitrary classifier over the set of $n$-by-$n$ images, we show that for all but one class it is possible to change the classification of all but a tiny fraction of the images in that class with a tiny modification compared to the diameter of the image space when measured in any $p$-norm, including the hamming distance. We then examine how this phenomenon manifests in human visual perception and discuss its implications for the design considerations of computer vision systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge