Image classification and retrieval with random depthwise signed convolutional neural networks

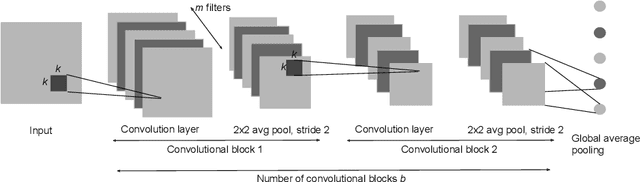
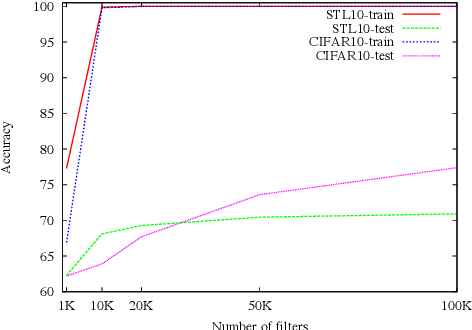
We study image classification and retrieval performance in a feature space given by random depthwise convolutional neural networks. Intuitively our network can be interpreted as applying random hyperplanes to the space of all patches of input images followed by average pooling to obtain final features. We show that the ratio of image pixel distribution similarity across classes to within classes and the average margin of the linear support vector machine on test data are both higher in our network's final layer compared to the input space. We then apply the linear support vector machine for image classification and $k$-nearest neighbor for image similarity detection on our network's final layer. We show that for classification our network attains higher accuracies than previous random networks and is not far behind in accuracy to trained state of the art networks, especially in the top-k setting. For example the top-2 accuracy of our network is near 90\% on both CIFAR10 and a 10-class mini ImageNet, and 85\% on STL10. In the problem of image similarity we find that $k$-nearest neighbor gives a comparable precision on the Corel Princeton Image Similarity Benchmark than if we were to use the last hidden layer of trained networks. We highlight sensitivity of our network to background color as a potential pitfall. Overall our work pushes the boundary of what can be achieved with random weights.