Identification of individual coherent sets associated with flow trajectories using Coherent Structure Coloring
Paper and Code
Aug 18, 2017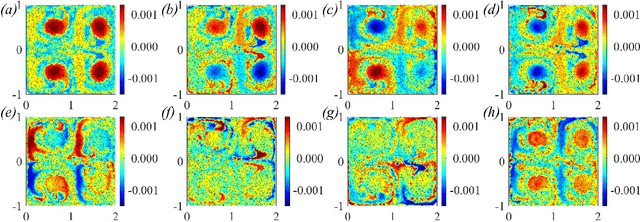
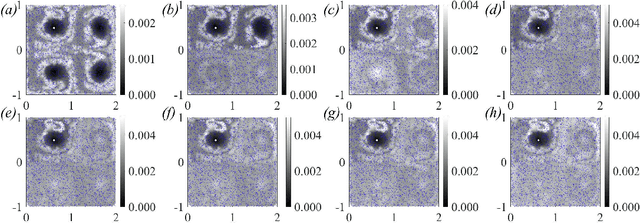
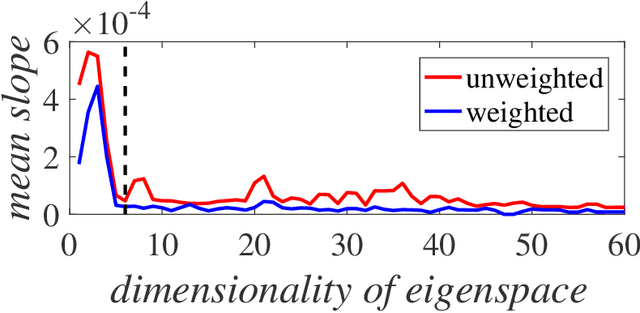
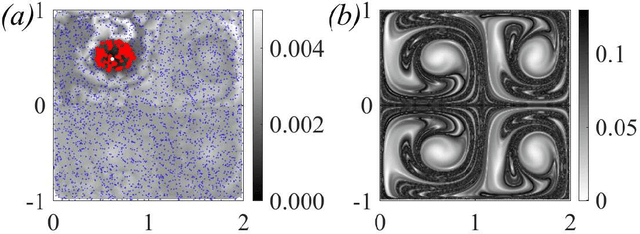
We present a method for identifying the coherent structures associated with individual Lagrangian flow trajectories even where only sparse particle trajectory data is available. The method, based on techniques in spectral graph theory, uses the Coherent Structure Coloring vector and associated eigenvectors to analyze the distance in higher-dimensional eigenspace between a selected reference trajectory and other tracer trajectories in the flow. By analyzing this distance metric in a hierarchical clustering, the coherent structure of which the reference particle is a member can be identified. This algorithm is proven successful in identifying coherent structures of varying complexities in canonical unsteady flows. Additionally, the method is able to assess the relative coherence of the associated structure in comparison to the surrounding flow. Although the method is demonstrated here in the context of fluid flow kinematics, the generality of the approach allows for its potential application to other unsupervised clustering problems in dynamical systems such as neuronal activity, gene expression, or social networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge