HyperNets and their application to learning spatial transformations
Paper and Code
Jul 12, 2018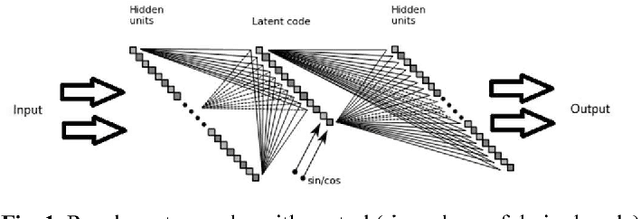

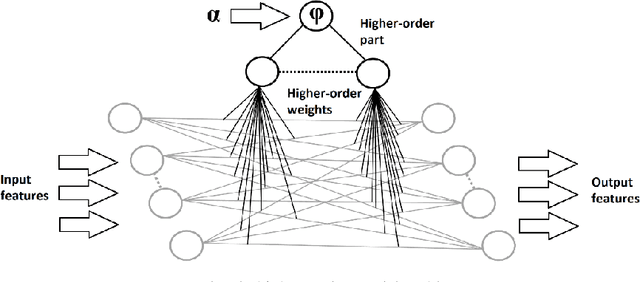
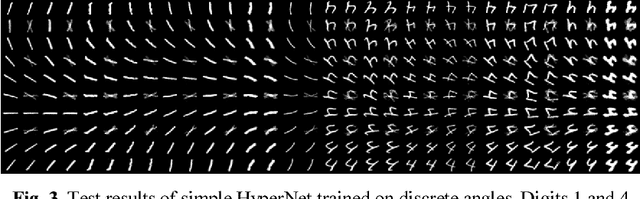
In this paper we propose a conceptual framework for higher-order artificial neural networks. The idea of higher-order networks arises naturally when a model is required to learn some group of transformations, every element of which is well-approximated by a traditional feedforward network. Thus the group as a whole can be represented as a hyper network. One of typical examples of such groups is spatial transformations. We show that the proposed framework, which we call HyperNets, is able to deal with at least two basic spatial transformations of images: rotation and affine transformation. We show that HyperNets are able not only to generalize rotation and affine transformation, but also to compensate the rotation of images bringing them into canonical forms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge