Hyperbolic Metric Learning for Visual Outlier Detection
Paper and Code
Mar 22, 2024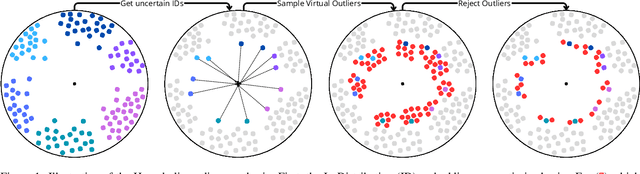
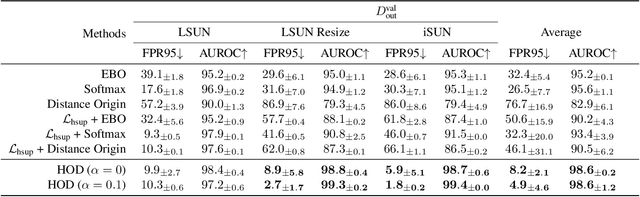
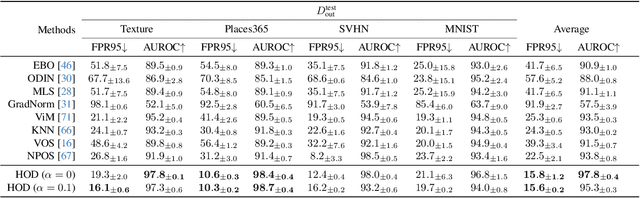
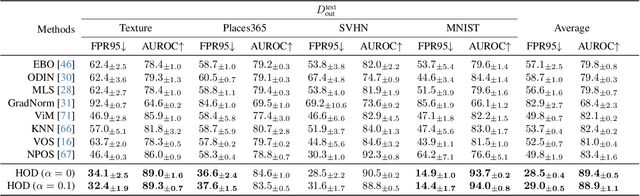
Out-Of-Distribution (OOD) detection is critical to deploy deep learning models in safety-critical applications. However, the inherent hierarchical concept structure of visual data, which is instrumental to OOD detection, is often poorly captured by conventional methods based on Euclidean geometry. This work proposes a metric framework that leverages the strengths of Hyperbolic geometry for OOD detection. Inspired by previous works that refine the decision boundary for OOD data with synthetic outliers, we extend this method to Hyperbolic space. Interestingly, we find that synthetic outliers do not benefit OOD detection in Hyperbolic space as they do in Euclidean space. Furthermore we explore the relationship between OOD detection performance and Hyperbolic embedding dimension, addressing practical concerns in resource-constrained environments. Extensive experiments show that our framework improves the FPR95 for OOD detection from 22\% to 15\% and from 49% to 28% on CIFAR-10 and CIFAR-100 respectively compared to Euclidean methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge