Hybrid Feedback for Global Attitude Tracking
Paper and Code
Dec 23, 2020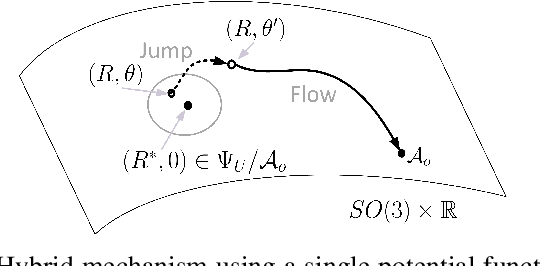
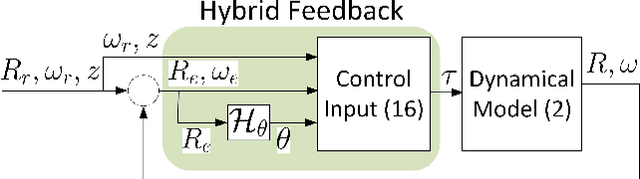
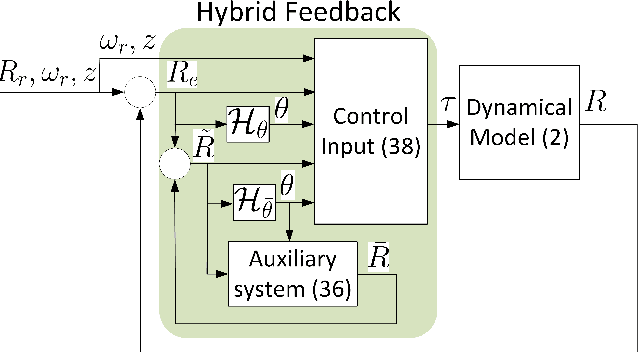
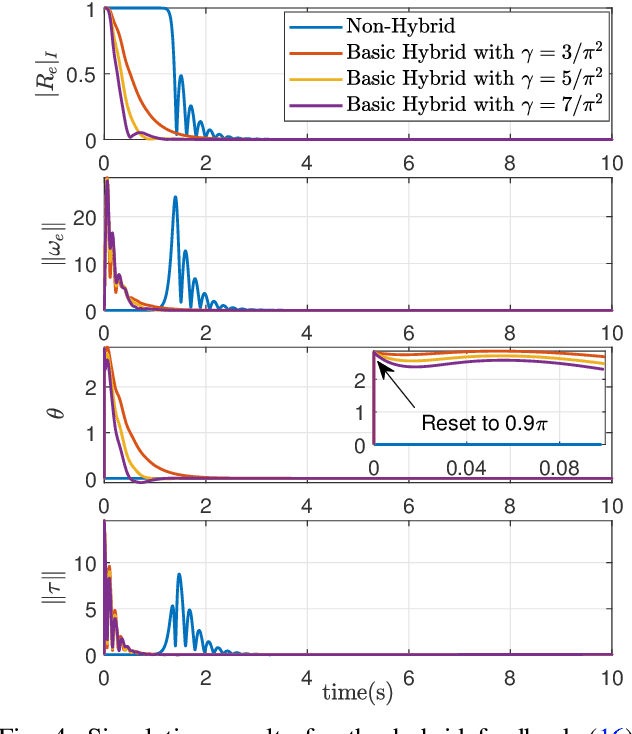
We introduce a new hybrid control strategy, which is conceptually different from the commonly used synergistic hybrid approaches, to efficiently deal with the problem of the undesired equilibria that precludes smooth vectors fields on $SO(3)$ from achieving global stability. The key idea consists in constructing a suitable potential function on $SO(3)\times \mathbb{R}$ involving an auxiliary scalar variable, with flow and jump dynamics, which keeps the state away from the undesired critical points while, at the same time, guarantees a decrease of the potential function over the flows and jumps. Based on this new hybrid mechanism, a hybrid feedback control scheme for the attitude tracking problem on $SO(3)$, endowed with global asymptotic stability and semi-global exponential stability guarantees, is proposed. This control scheme is further improved through a smoothing mechanism that removes the discontinuities in the input torque. The third hybrid control scheme, proposed in this paper, removes the requirement of the angular velocity measurements, while preserving the strong stability guarantees of the first hybrid control scheme. Finally, some simulation results are presented to illustrate the performance of the proposed hybrid controllers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge