How Sampling Impacts the Robustness of Stochastic Neural Networks

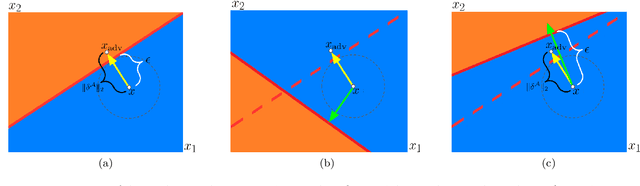
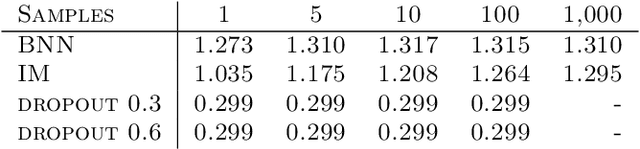
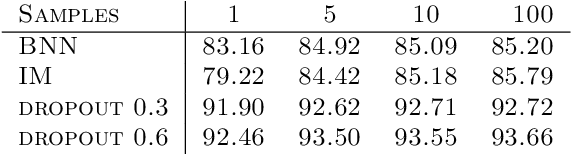
Stochastic neural networks (SNNs) are random functions and predictions are gained by averaging over multiple realizations of this random function. Consequently, an adversarial attack is calculated based on one set of samples and applied to the prediction defined by another set of samples. In this paper we analyze robustness in this setting by deriving a sufficient condition for the given prediction process to be robust against the calculated attack. This allows us to identify the factors that lead to an increased robustness of SNNs and helps to explain the impact of the variance and the amount of samples. Among other things, our theoretical analysis gives insights into (i) why increasing the amount of samples drawn for the estimation of adversarial examples increases the attack's strength, (ii) why decreasing sample size during inference hardly influences the robustness, and (iii) why a higher prediction variance between realizations relates to a higher robustness. We verify the validity of our theoretical findings by an extensive empirical analysis.