How Nonconformity Functions and Difficulty of Datasets Impact the Efficiency of Conformal Classifiers
Paper and Code
Aug 12, 2021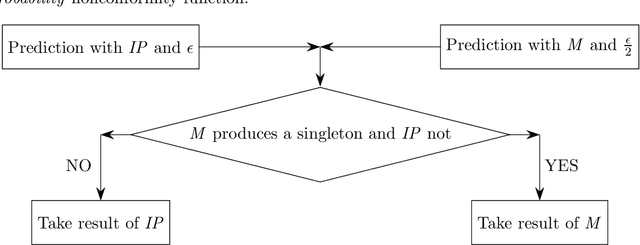

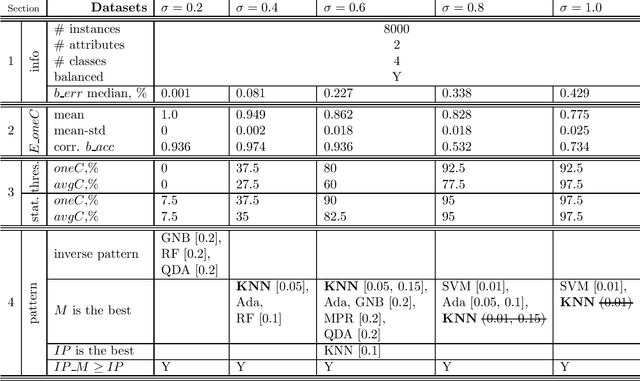
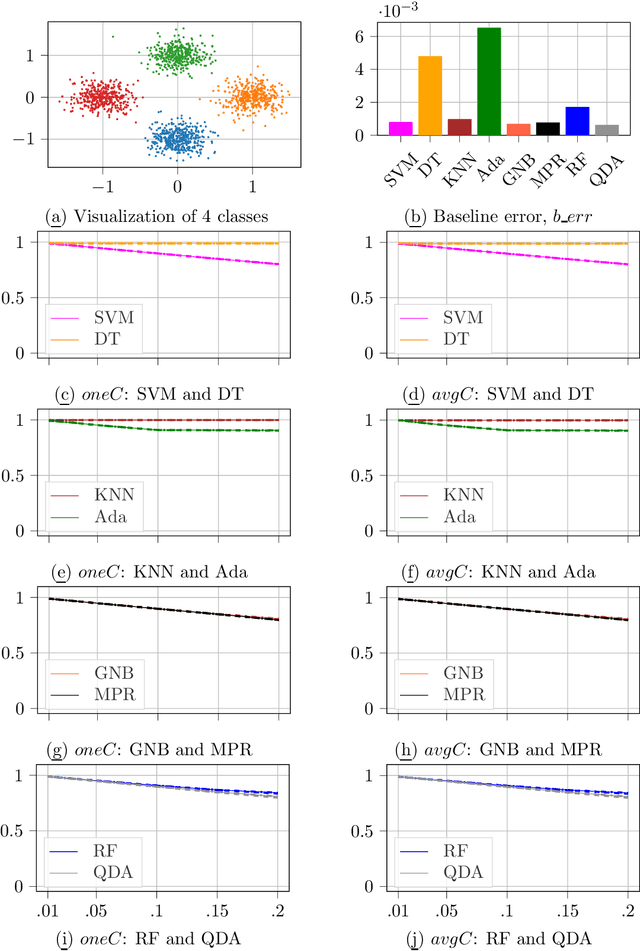
The property of conformal predictors to guarantee the required accuracy rate makes this framework attractive in various practical applications. However, this property is achieved at a price of reduction in precision. In the case of conformal classification, the systems can output multiple class labels instead of one. It is also known from the literature, that the choice of nonconformity function has a major impact on the efficiency of conformal classifiers. Recently, it was shown that different model-agnostic nonconformity functions result in conformal classifiers with different characteristics. For a Neural Network-based conformal classifier, the inverse probability (or hinge loss) allows minimizing the average number of predicted labels, and margin results in a larger fraction of singleton predictions. In this work, we aim to further extend this study. We perform an experimental evaluation using 8 different classification algorithms and discuss when the previously observed relationship holds or not. Additionally, we propose a successful method to combine the properties of these two nonconformity functions. The experimental evaluation is done using 11 real and 5 synthetic datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge