Higher-Degree Stochastic Integration Filtering
Paper and Code
Aug 01, 2016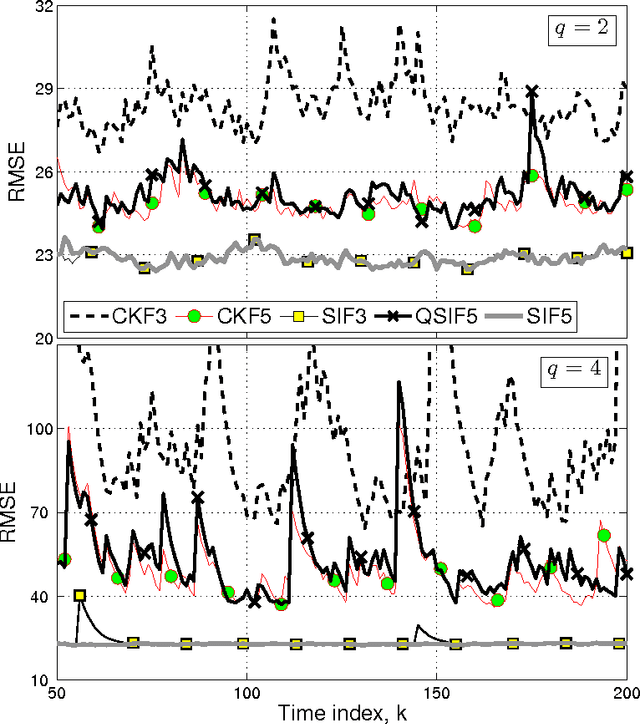

We obtain a class of higher-degree stochastic integration filters (SIF) for nonlinear filtering applications. SIF are based on stochastic spherical-radial integration rules that achieve asymptotically exact evaluations of Gaussian weighted multivariate integrals found in nonlinear Bayesian filtering. The superiority of the proposed scheme is demonstrated by comparing the performance of the proposed fifth-degree SIF against a number of existing stochastic, quasi-stochastic and cubature (Kalman) filters. The proposed filter is demonstrated to outperform existing filters in all cases.
* Submitted to IEEE Signal Processing Letters on 17th July 2016
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge