High-dimensional Nonlinear Profile Monitoring based on Deep Probabilistic Autoencoders

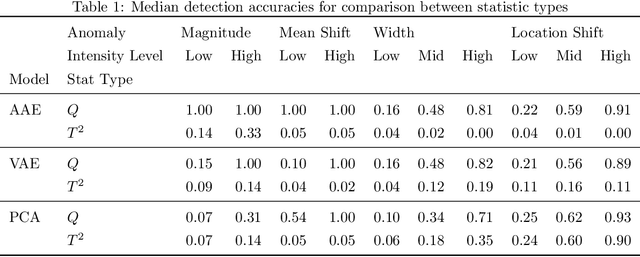
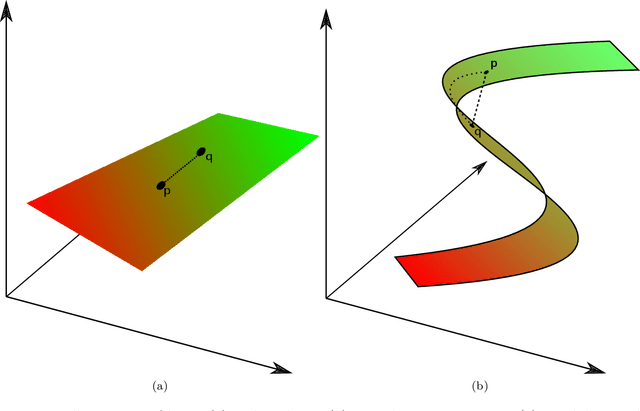
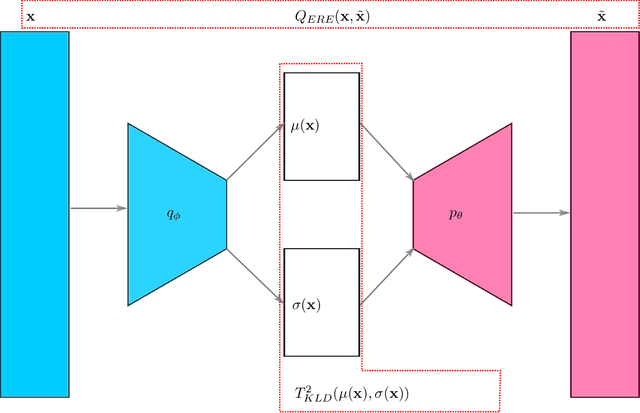
Wide accessibility of imaging and profile sensors in modern industrial systems created an abundance of high-dimensional sensing variables. This led to a a growing interest in the research of high-dimensional process monitoring. However, most of the approaches in the literature assume the in-control population to lie on a linear manifold with a given basis (i.e., spline, wavelet, kernel, etc) or an unknown basis (i.e., principal component analysis and its variants), which cannot be used to efficiently model profiles with a nonlinear manifold which is common in many real-life cases. We propose deep probabilistic autoencoders as a viable unsupervised learning approach to model such manifolds. To do so, we formulate nonlinear and probabilistic extensions of the monitoring statistics from classical approaches as the expected reconstruction error (ERE) and the KL-divergence (KLD) based monitoring statistics. Through extensive simulation study, we provide insights on why latent-space based statistics are unreliable and why residual-space based ones typically perform much better for deep learning based approaches. Finally, we demonstrate the superiority of deep probabilistic models via both simulation study and a real-life case study involving images of defects from a hot steel rolling process.