Hierarchical Reinforcement Learning via Advantage-Weighted Information Maximization
Paper and Code
Jan 05, 2019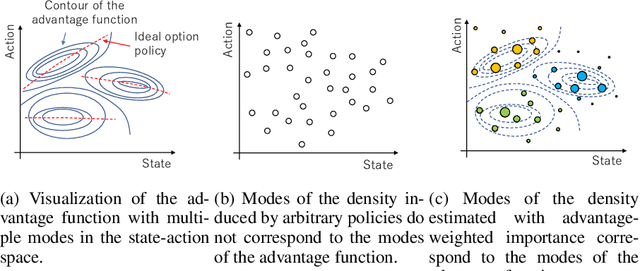


Real-world tasks are often highly structured. Hierarchical reinforcement learning (HRL) has attracted research interest as an approach for leveraging the hierarchical structure of a given task in reinforcement learning (RL). However, identifying the hierarchical policy structure that enhances the performance of RL is not a trivial task. In this paper, we propose an HRL method that learns a latent variable of a hierarchical policy using mutual information maximization. Our approach can be interpreted as a way to learn a discrete and latent representation of the state-action space. To learn option policies that correspond to modes of the advantage function, we introduce advantage-weighted importance sampling. In our HRL method, the gating policy learns to select option policies based on an option-value function, and these option policies are optimized based on the deterministic policy gradient method. This framework is derived by leveraging the analogy between a monolithic policy in standard RL and a hierarchical policy in HRL by using a deterministic option policy. Experimental results indicate that our HRL approach can learn a diversity of options and that it can enhance the performance of RL in continuous control tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge