Heterogeneous Treatment Effect Estimation for Observational Data using Model-based Forests
Paper and Code
Oct 06, 2022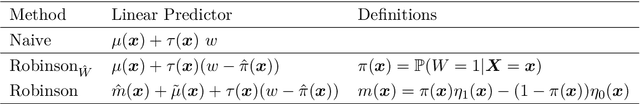
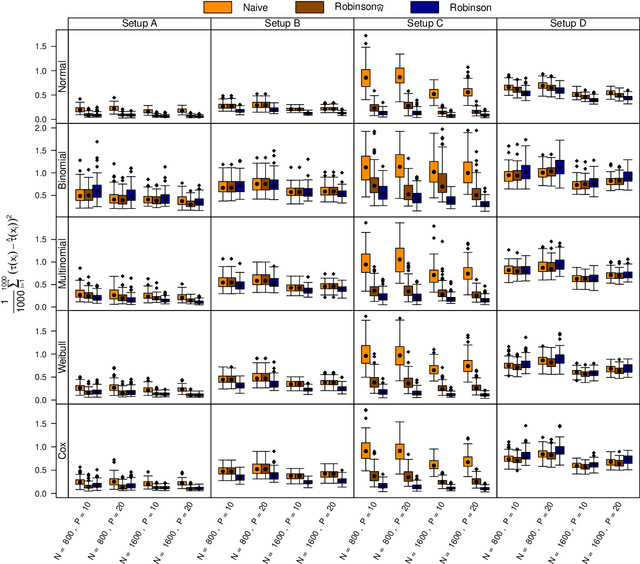
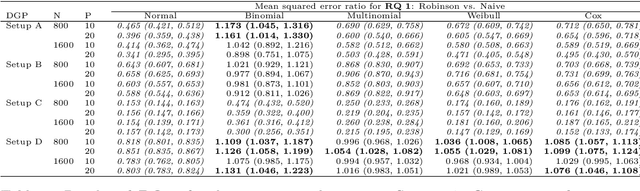
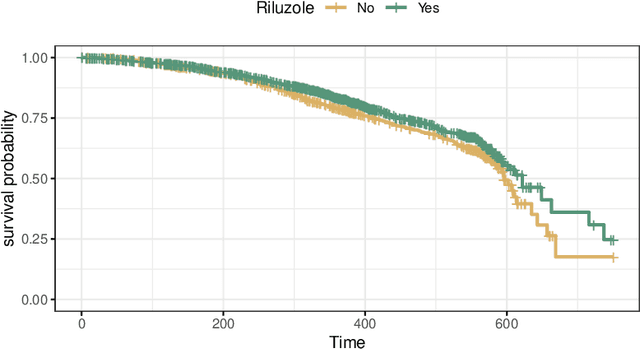
The estimation of heterogeneous treatment effects (HTEs) has attracted considerable interest in many disciplines, most prominently in medicine and economics. Contemporary research has so far primarily focused on continuous and binary responses where HTEs are traditionally estimated by a linear model, which allows the estimation of constant or heterogeneous effects even under certain model misspecifications. More complex models for survival, count, or ordinal outcomes require stricter assumptions to reliably estimate the treatment effect. Most importantly, the noncollapsibility issue necessitates the joint estimation of treatment and prognostic effects. Model-based forests allow simultaneous estimation of covariate-dependent treatment and prognostic effects, but only for randomized trials. In this paper, we propose modifications to model-based forests to address the confounding issue in observational data. In particular, we evaluate an orthogonalization strategy originally proposed by Robinson (1988, Econometrica) in the context of model-based forests targeting HTE estimation in generalized linear models and transformation models. We found that this strategy reduces confounding effects in a simulated study with various outcome distributions. We demonstrate the practical aspects of HTE estimation for survival and ordinal outcomes by an assessment of the potentially heterogeneous effect of Riluzole on the progress of Amyotrophic Lateral Sclerosis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge