Hamiltonian prior to Disentangle Content and Motion in Image Sequences
Paper and Code
Dec 02, 2021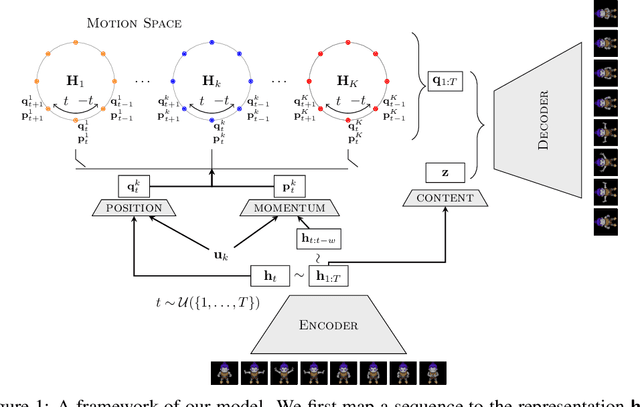
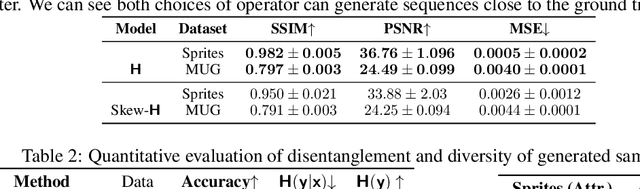


We present a deep latent variable model for high dimensional sequential data. Our model factorises the latent space into content and motion variables. To model the diverse dynamics, we split the motion space into subspaces, and introduce a unique Hamiltonian operator for each subspace. The Hamiltonian formulation provides reversible dynamics that learn to constrain the motion path to conserve invariant properties. The explicit split of the motion space decomposes the Hamiltonian into symmetry groups and gives long-term separability of the dynamics. This split also means representations can be learnt that are easy to interpret and control. We demonstrate the utility of our model for swapping the motion of two videos, generating sequences of various actions from a given image and unconditional sequence generation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge