Greedy Sensor Placement for Weighted Linear-Least Squares Estimation under Correlated Noise

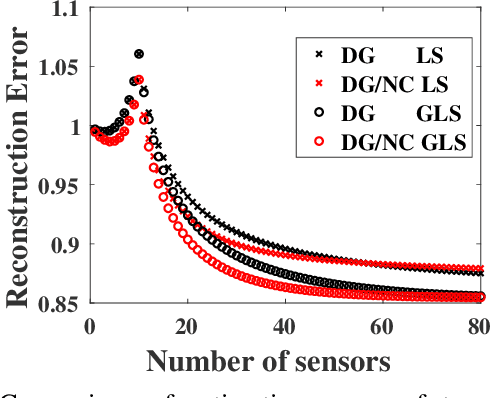
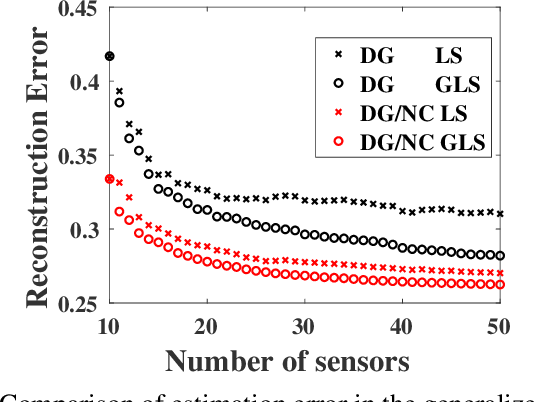
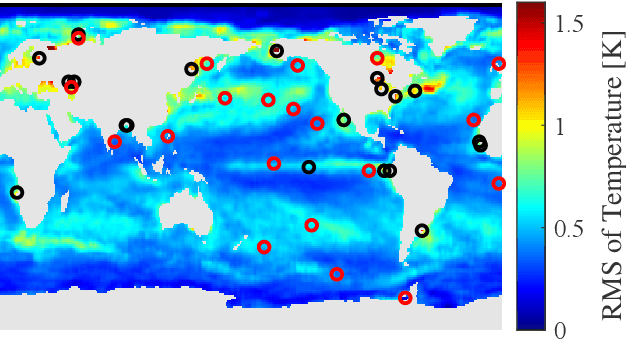
Optimization for sensor placement has been intensely studied to monitor complex, large scale systems, whereas one needs to overcome its intractable nature of the objective function for the optimization. In this study, a fast algorithm for greedy sensor selection is presented for a linear reduced-ordered reconstruction under the assumption of correlated noise on the sensor signals. The presented algorithm accomplishes the maximization of the determinant of the Fisher information matrix in the linear inverse problem, while this study firstly shows that the objective function with correlated noise is neither submodular nor supermodular. Efficient one-rank computations in the greedy selection procedure are introduced in both of the underdetermined and oversampled problem. Several numerical experiments show the effectiveness of the selection algorithm for its accuracy in the estimation of the states of large dimensional measurement data.