Gradient-based Counterfactual Explanations using Tractable Probabilistic Models
Paper and Code
May 16, 2022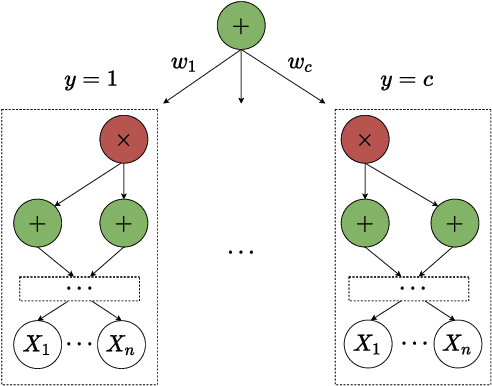

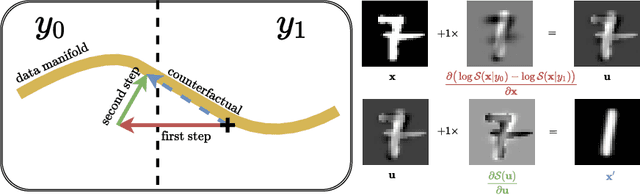
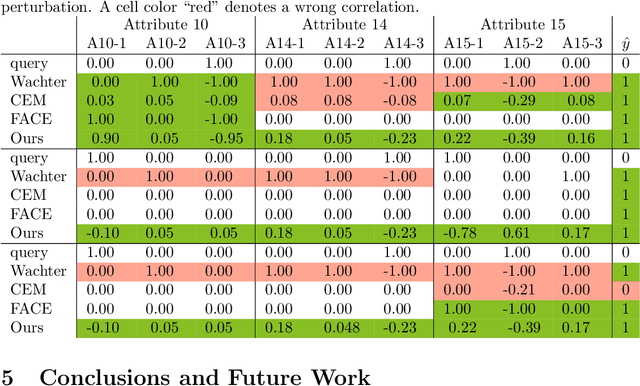
Counterfactual examples are an appealing class of post-hoc explanations for machine learning models. Given input $x$ of class $y_1$, its counterfactual is a contrastive example $x^\prime$ of another class $y_0$. Current approaches primarily solve this task by a complex optimization: define an objective function based on the loss of the counterfactual outcome $y_0$ with hard or soft constraints, then optimize this function as a black-box. This "deep learning" approach, however, is rather slow, sometimes tricky, and may result in unrealistic counterfactual examples. In this work, we propose a novel approach to deal with these problems using only two gradient computations based on tractable probabilistic models. First, we compute an unconstrained counterfactual $u$ of $x$ to induce the counterfactual outcome $y_0$. Then, we adapt $u$ to higher density regions, resulting in $x^{\prime}$. Empirical evidence demonstrates the dominant advantages of our approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge