GP-RVM: Genetic Programing-based Symbolic Regression Using Relevance Vector Machine
Paper and Code
Aug 26, 2018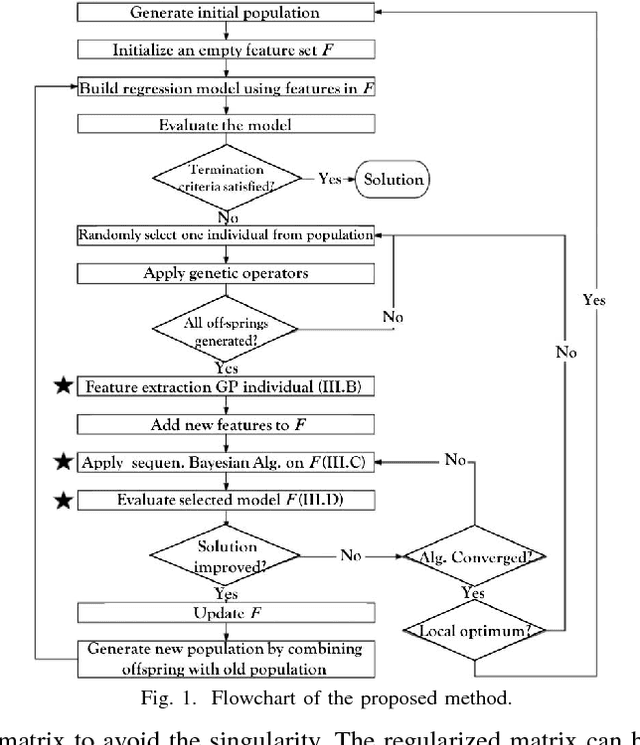
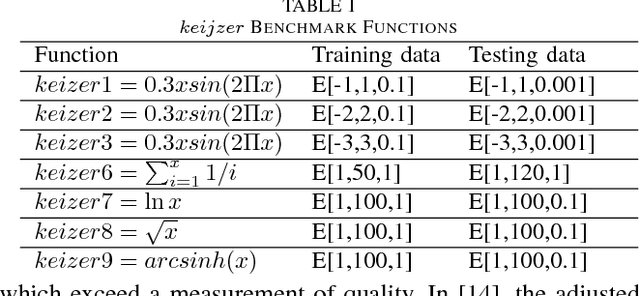
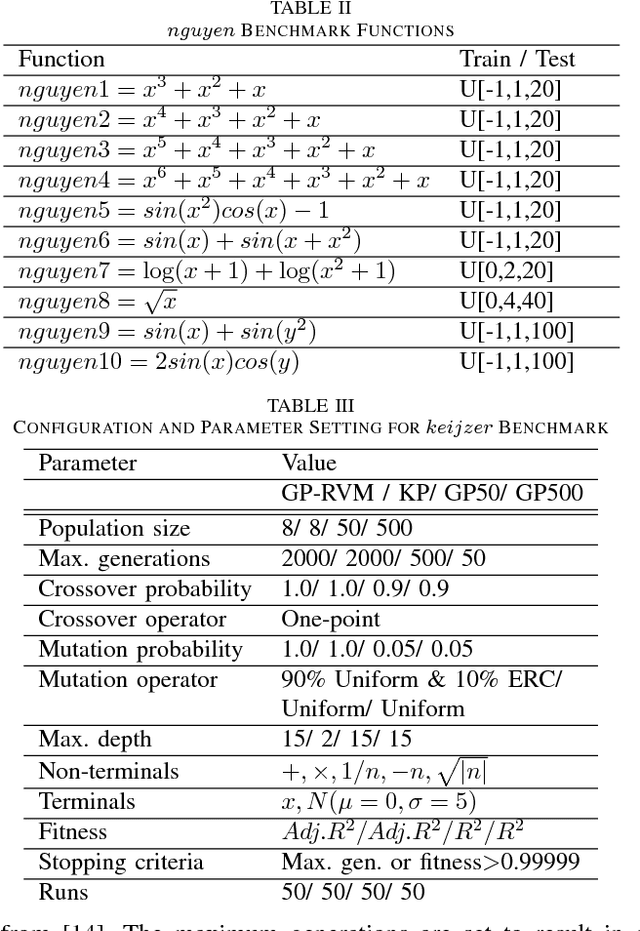

This paper proposes a hybrid basis function construction method (GP-RVM) for Symbolic Regression problem, which combines an extended version of Genetic Programming called Kaizen Programming and Relevance Vector Machine to evolve an optimal set of basis functions. Different from traditional evolutionary algorithms where a single individual is a complete solution, our method proposes a solution based on linear combination of basis functions built from individuals during the evolving process. RVM which is a sparse Bayesian kernel method selects suitable functions to constitute the basis. RVM determines the posterior weight of a function by evaluating its quality and sparsity. The solution produced by GP-RVM is a sparse Bayesian linear model of the coefficients of many non-linear functions. Our hybrid approach is focused on nonlinear white-box models selecting the right combination of functions to build robust predictions without prior knowledge about data. Experimental results show that GP-RVM outperforms conventional methods, which suggest that it is an efficient and accurate technique for solving SR. The computational complexity of GP-RVM scales in $O( M^{3})$, where $M$ is the number of functions in the basis set and is typically much smaller than the number $N$ of training patterns.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge